��Ŀ����
4���ⷽ���顢�ⲻ��ʽ�鲢�ѽ⼯��ʾ�������ϱ�ʾ��1��$\left\{\begin{array}{l}{3��m+n��+4��m-n��=15}\\{\frac{m+n}{2}+\frac{m-n}{6}=1}\end{array}\right.$
��2��$\left\{\begin{array}{l}{5x-6��2��x+3��}\\{\frac{x}{4}-1��\frac{x-3}{3}}\end{array}\right.$��
���� ��1�����������������ô�����Ԫ������⼴�ɣ�
��2���ֱ��������ʽ����������ʽ�Ľ⼯���ҳ����⼯�Ĺ������֣�����ȷ��������ʽ��Ľ⼯����ʾ�������ϼ��ɣ�
��� �⣺��1�������������ã�$\left\{\begin{array}{l}{7m-n=15��}\\{2m+n=3��}\end{array}\right.$��
��+�ٵã�9m=18����m=2��
��m=2����ڵã�n=-1��
����Ľ�Ϊ$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$��
��2��$\left\{\begin{array}{l}{5x-6��2��x+3����}\\{\frac{x}{4}-1��\frac{x-3}{3}��}\end{array}\right.$��
�ɢٵã�x��4��
�ɢڵã�x��0��
�ʲ���ʽ��Ľ⼯Ϊ0��x��4��
��ʾ�������ϣ���ͼ��ʾ��
���� ���⿼���˶�Ԫһ�η����飬һԪһ�β���ʽ��Ľⷨ�����н��Ԫһ�η�����ķ�����������Ԫ���ͼӼ���Ԫ��������ʽ��ȡ�⼯�ķ���Ϊ��ͬ��ȡ��ͬСȡС����СС��ȥ�м䣻���СС�⣮

��ϰ��ϵ�д�
�����Ŀ
14����A��-4��y1����B��2��y2������ֱ��y=-x-1�ϣ���y1��y2�Ĵ�С��ϵΪ��������
| A�� | y1��y2 | B�� | y1=y2 | C�� | y1��y2 | D�� | ��ȷ�� |
19������˵������ȷ���ǣ�������
| A�� | x=3��y=2�Ƿ���3x-4y=1��һ��� | |
| B�� | ����3x-4y=1��������⣬��x��y����ȡ�κ���ֵ | |
| C�� | ����3x-4y=1ֻ������⣬������ǣ�$\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | |
| D�� | ����3x-4y=1������ |
16�����ξ��ж�ƽ���ı��β�һ�����е������ǣ�������
| A�� | �ڽǺ���360�� | B�� | �Խ������ | C�� | �Ա�ƽ������� | D�� | �Խ����ഹֱ |
13����0��-1.5��1��-2�ĸ����У���С�����ǣ�������
| A�� | 0 | B�� | 1 | C�� | -2 | D�� | -1.5 |
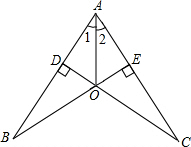 ��ͼ��CD��AB��BE��AC������ֱ�ΪD��E��BE��CD���ڵ�O��OB=OC����֤����1=��2��
��ͼ��CD��AB��BE��AC������ֱ�ΪD��E��BE��CD���ڵ�O��OB=OC����֤����1=��2�� ��1��������ABC����y��ԳƵġ�A1B1C1����д����A1B1C1�ĸ���������꣮
��1��������ABC����y��ԳƵġ�A1B1C1����д����A1B1C1�ĸ���������꣮