题目内容
1. 如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是∠OEP=∠ODP或∠OEP+∠ODP=180°.
如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是∠OEP=∠ODP或∠OEP+∠ODP=180°.
分析 以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,根据SAS证△E2OP≌△DOP,推出E2P=PD,得出此时点E2符合条件,此时∠OE2P=∠ODP;以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,根据等腰三角形性质推出∠PE2E1=∠PE1E2,求出∠OE1P+∠ODP=180°即可.
解答 解:∠OEP=∠ODP或∠OEP+∠ODP=180°,理由如下: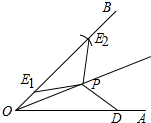
以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,如图所示:
∵在△E2OP和△DOP中,$\left\{\begin{array}{l}{O{E}_{2}=OD}&{\;}\\{∠{E}_{2}OP=∠DOP}&{\;}\\{OP=OP}&{\;}\end{array}\right.$,
∴△E2OP≌△DOP(SAS),
∴E2P=PD,
即此时点E2符合条件,此时∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°,
故答案为:∠OEP=∠ODP或∠OEP+∠ODP=180°.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质和判定等知识点,主要考查学生的猜想能力和分析问题和解决问题的能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9. 如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的点是( )
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的点是( )
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的点是( )| A. | 点A与点D | B. | 点A与点C | C. | 点B与点D | D. | 点B与点C |
 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a-b+c<0,③2a+b=0,④b2-4ac>0,其中正确结论个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a-b+c<0,③2a+b=0,④b2-4ac>0,其中正确结论个数是( ) 如图,OD、OE分别是∠AOC和∠BOC的平分线,∠AOD=40°,∠BOE=25°,求∠AOB的度数.
如图,OD、OE分别是∠AOC和∠BOC的平分线,∠AOD=40°,∠BOE=25°,求∠AOB的度数. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△OAB和△OA1B1(顶点是网格线的交点).点A、B坐标为(-1,0),(-1,2).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△OAB和△OA1B1(顶点是网格线的交点).点A、B坐标为(-1,0),(-1,2). 如图,某同学身高AB=1.60米,他从路灯底部的D点处沿直线前进4米到点B时,其影长PB=2米,求路灯杆CD的高度.
如图,某同学身高AB=1.60米,他从路灯底部的D点处沿直线前进4米到点B时,其影长PB=2米,求路灯杆CD的高度.