题目内容

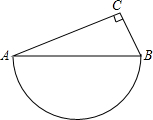如图，在直角三角形ABC中，∠C=90°，AC=12，BC=5，则以AB为直径的半圆的面积为
 
．
考点：勾股定理
专题：
分析：利用勾股定理列式求出AB，再根据圆的面积公式列式计算即可得解．
解答：解：∵∠C=90°，AC=12，BC=5，
∴AB=
AC2+BC2
=
122+52
=13，
∴以AB为直径的半圆的面积=
1
2
π（
AB
2
）2=
1
2
π（
13
2
）2=
169
8
π．
故答案为：
169
8
π．
点评：本题考查了勾股定理，圆的面积公式，熟记定理与公式是解题的关键，要注意AB是半圆的直径，而非半径．
练习册系列答案
相关题目
先化简，再求值：[2x2-（x+y）（x-y）]•[（-x-y）（y-x）+2y2]，其中x=1，y=-1．
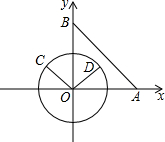如图，在平面直角坐标系xOy中，点A（4，0），点B（0，4），动点C在以半径为2的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），当AC与⊙O相切时，点D的坐标为
 
．
矩形ABCD沿对角线BD翻折BCD为BC′D，设C′B与AD交点为E，△BED面积为整个矩形面积的
1
3
，求∠DBC的度数．
用”＞”、”＜”、”=”连接下列两数：
|-
7
11
|
 
|
7
11
|，|-3.5|
 
-3.5，
|0|
 
|-0.58|，|-5.9|
 
|-6.2|，-
3
2
 
-
2
3
．
已知池中有600m3的水，每小时抽50m3．
（1）写出剩余水的体积Vm3与时间th之间的函数表达式；
（2）写出自变量t的取值范围；
（3）8h后，池中还剩多少水？
（4）多长时间后，池中剩余100m3的水？
（1）引入：如图1，直线AB为⊙O的弦，OC⊥OA，交AB于点P，且PC=BC，直线BC是否与⊙O相切，为什么？
（2）引申：记（1）中⊙O的切线为直线l，在（1）的条件下，如图2，将切线l向下平移，设平移后的直线l与OB的延长线相交于点B′，与AB的延长线相交于点E，与OP的延长线相交于点C′．
①找出图2中与C′P相等的线段，并说明理由；
②如果OB′=9cm，B′C′=12cm，⊙O的半径为6cm，试求线段B′E的长．
在坐标系中，P点的坐标是（cos30°，tan45°），则P点关于x轴对称点Q的坐标为（　　）
A、（
3
2
，1）
B、（-1，
3
2
）
C、（
3
2
，-1）
D、（-
3
2
，-1）
已知抛物线y=x2+2x+a与x轴的一个交点坐标为（-3，0），则此抛物线与x轴的另一个交点坐标为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网