题目内容
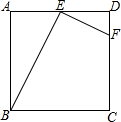如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且CF=3FD，△ABE与△DEF相似吗？为什么？考点：相似三角形的判定
专题：常规题型
分析：先根据正方形的性质得∠A=∠D=90°，AB=AD=CD，设AB=AD=CD=4a，利用E为边AD的中点，CF=3FD，得到AE=DE=2a，DF=a，则可计算出
=
=2，加上∠A=∠D，于是根据相似三角形的判定方法即可得到△ABE∽△DEF．
| AB |
| DE |
| AE |
| DF |
解答：解：△ABE与△DEF相似．理由如下：
∵四边形ABCD为正方形，
∴∠A=∠D=90°，AB=AD=CD，
设AB=AD=CD=4a，
∵E为边AD的中点，CF=3FD，
∴AE=DE=2a，DF=a，
∴
=
=2，
=
=2，
∴
=
，
而∠A=∠D，
∴△ABE∽△DEF．
∵四边形ABCD为正方形，
∴∠A=∠D=90°，AB=AD=CD，
设AB=AD=CD=4a，
∵E为边AD的中点，CF=3FD，
∴AE=DE=2a，DF=a，
∴
| AB |
| DE |
| 4a |
| 2a |
| AE |
| DF |
| 2a |
| a |
∴
| AB |
| DE |
| AE |
| DF |
而∠A=∠D，
∴△ABE∽△DEF．
点评：本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．也考查了正方形的性质．
练习册系列答案
相关题目
点P到△ABC三边的距离相等，则点P是（ ）的交点．
| A、中线 | B、高线 |
| C、垂直平分线 | D、角平分线 |
如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD：DB=3：1，AC=12，求EC的长度．
已知∠AOB=40°，∠AOB的余角为∠AOC，∠AOB的补角为∠BOD，OM平分∠AOC，ON平分∠BOD．