题目内容
11.已知顶点为A(2,-1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,0);(1)求这条抛物线的表达式;
(2)连接AB、BD、DA,求cos∠ABD的大小;
(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.
分析 (1)设抛物线的解析式为y=a(x-2)2-1,将点C的坐标代入可求得a的值,从而可得到抛物线的解析式;
(2)先求得点B、C、D的坐标,由点A、B、D的坐标可得到∠BDO=∠ADO=45°,从而可证明△ABD为直角三角形,然后依据两点间的距离公式可求得AB和BD的长,最后依据余弦函数的定义求解即可;
(3)先证明△ADP∽△PDB,依据相似三角形的性质可得到DP2=BD•AD,从而可求得DP的长,故此可得到点P的坐标.
解答 解:(1)设抛物线的解析式为y=a(x-2)2-1,将点C的坐标代入得:a-1=0,解得a=1,
∴抛物线的解析式为y=(x-2)2-1,即y=x2-4x+3.
(2)如图1所示: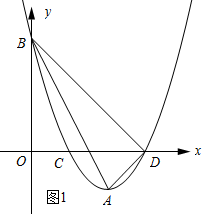
令y=0得:x2-4x+3=0,解得:x=1或x=3,
∴C(1,0)、D(3,0).
令x=0得y=3,
∴B(0,3).
∴OB=OD.
∴∠BDO=45°.
∵A(2,-1),D(3,0),
∴∠ADO=45°,
∴∠ADB=90°.
依据两点间的距离公式可知AB=2$\sqrt{5}$,DB=3$\sqrt{2}$.
∴cos∠ABD=$\frac{BD}{AB}$=$\frac{3\sqrt{2}}{2\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
(3)如图2所示: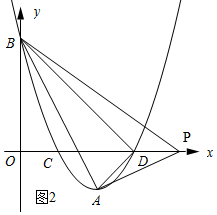
∵∠BPD+∠PBD=∠BDO=45°,∠BPD+∠DPA=45°,
∴∠DBP=∠DOA.
∵∠APD+∠DAP=∠ADO=45°,∠BPD+∠DPA=45°,
∴∠DAP=∠DBP.
∴△ADP∽△PDB.
∴$\frac{DP}{AD}$=$\frac{BD}{DP}$,即DP2=BD•AD.
∵AD=$\sqrt{2}$,BD=3$\sqrt{2}$,
∴DP2=6.
∴DP=$\sqrt{6}$.
∴OP=2+$\sqrt{6}$.
∴点P的坐标为(3+$\sqrt{6}$,0).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、锐角三角函数的定义、相似三角形的性质和判断,证得△ABD为直角三角形是解答问题(2)的关键;证得△ADP∽△PDB是解答问题(3)的关键.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案| A. | 1 | B. | 5 | C. | -5 | D. | -1 |
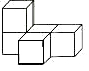 如图所示的几何体是由五个完全相同且棱长为1的正方体组成的,下列关于这个几何体的说法正确的是( )
如图所示的几何体是由五个完全相同且棱长为1的正方体组成的,下列关于这个几何体的说法正确的是( )| A. | 主视图的面积为5 | B. | 俯视图的面积为3 | ||
| C. | 左视图的面积为3 | D. | 三个视图的面积都为4 |
| A. | (a-b)2=a2-b2 | B. | (2a+b)(-2a+b)=2a2-b2 | ||
| C. | (a+1)(a-2)=a2-2 | D. | (-a-b)2=a2+2ab+b2 |
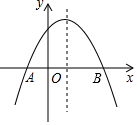 如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )
如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )