题目内容
19.先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去一层根号.
例如:$\sqrt{3+2\sqrt{2}}$=$\sqrt{3+2×1×\sqrt{2}}$=$\sqrt{{1}^{2}+(\sqrt{2})^{2}+2×1×\sqrt{2}}$=$\sqrt{(1+\sqrt{2})^{2}}$=|1+$\sqrt{2}$|=1+$\sqrt{2}$
解决问题:
①模仿上例的过程填空:
$\sqrt{14+6\sqrt{5}}$=$\sqrt{14+2×3×\sqrt{5}}$=$\sqrt{{3}^{2}+2×3×\sqrt{5}+(\sqrt{5})^{2}}$=$\sqrt{(3+\sqrt{5})^{2}}$=|3+$\sqrt{5}$|=3+$\sqrt{5}$
②根据上述思路,试将下列各式化简.
(1)$\sqrt{28-10\sqrt{3}}$ (2)$\sqrt{1+\frac{{\sqrt{3}}}{2}}$.
分析 ①模仿阅读材料的方法将原式变形,计算即可得到结果;
②仿照以上方法将各式化简即可.
解答 解:①原式=$\sqrt{14+2×3×\sqrt{5}}$=$\sqrt{{3}^{2}+2×3×\sqrt{5}+(\sqrt{5})^{2}}$=$\sqrt{(3+\sqrt{5})^{2}}$=|3+$\sqrt{5}$|=3+$\sqrt{5}$;
故答案为:$\sqrt{{3}^{2}+2×3×\sqrt{5}+(\sqrt{5})^{2}}$;$\sqrt{(3+\sqrt{5})^{2}}$;|3+$\sqrt{5}$|;3+$\sqrt{5}$;
②(1)原式=$\sqrt{{5}^{2}-2×5×\sqrt{3}+(\sqrt{3})^{2}}$=$\sqrt{(5-\sqrt{3})^{2}}$=|5-$\sqrt{3}$|=5-$\sqrt{3}$;
(2)原式=$\sqrt{(\frac{1}{2})^{2}+2×\frac{1}{2}×\frac{\sqrt{3}}{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{(\frac{1}{2}+\frac{\sqrt{3}}{2})^{2}}$=|$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$|=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$.
点评 此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.计算a2•($\frac{1}{a}$)3的结果是( )
| A. | a | B. | a5 | C. | $\frac{1}{a}$ | D. | $\frac{1}{{a}^{5}}$ |
8.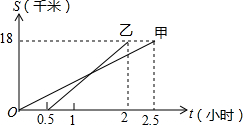 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )| A. | 乙比甲先到达B地 | B. | 乙在行驶过程中没有追上甲 | ||
| C. | 乙比甲早出发半小时 | D. | 甲的行驶速度比乙的行驶速度快 |
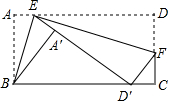 如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.
如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.