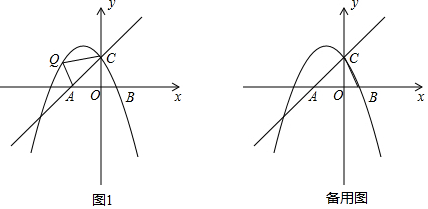
题目内容
16.如图,已知△ABC内接于⊙O,AD为边上的高,将△ADC沿直线AC翻折得到△AEC,延长EA交⊙O于点P,连接FC,交AB于N.(1)求证:∠BAC=∠ABC+∠ACF;
(2)求证:EF=DB;
(3)若AD=5,CD=10,CB∥AF,求点F到AB的距离.
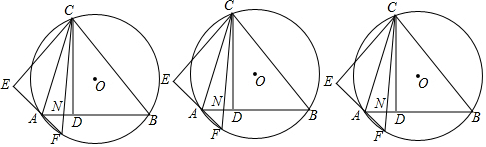
分析 (1)由△ADC沿直线AC翻折得到△AEC,可得∠BAC=∠EAC=∠ACF+∠F,又∠F=∠ABC,即可推出∠BAC=∠ABC+∠ACF;
(2)只要证明△CEF≌△CDB,即可推出EF=BD;
(3)首先证明tan∠EGA=tanB=tan∠BAF=$\frac{4}{3}$,设AF=a,BD=EF=5+a,构建tanB=$\frac{CD}{BD}$=$\frac{10}{5+a}$=$\frac{4}{3}$,推出a=$\frac{5}{2}$,在Rt△AMF中,构建tan∠FAM=$\frac{FM}{AM}$=$\frac{4}{3}$,即可推出AF=$\frac{5}{2}$,即可解决问题;
解答 (1)证明:如图1中,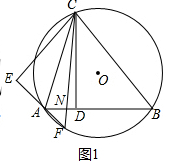 ∵△ADC沿直线AC翻折得到△AEC,
∵△ADC沿直线AC翻折得到△AEC,
∴∠BAC=∠EAC=∠ACF+∠F,
∵∠F=∠ABC,
∴∠BAC=∠ABC+∠ACF.
(2)在△CEF和△CDB中,
$\left\{\begin{array}{l}{∠F=∠B}\\{∠E=∠CDB}\\{CE=CD}\end{array}\right.$
∴△CEF≌△CDB,
∴EF=BD.
(3)由四边形AECD,可证得∠BAF=∠ECD=2∠ACD,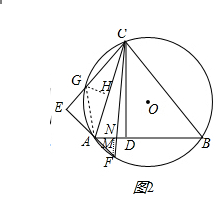
取AC中点H作HG⊥AC,交CE于点G,则GC=GA,
∴∠EGA=2∠GCA=∠ECD,
设GC=GA=x,则EG=10-x,
在Rt△AEG中,52+(10-x)2=x2,
∴x=$\frac{25}{4}$,
∴tan∠EGA=$\frac{4}{3}$,
∵BC∥AF,
tanB=tan∠BAF=$\frac{4}{3}$,
设AF=a,BD=EF=5+a
tanB=$\frac{CD}{BD}$=$\frac{10}{5+a}$=$\frac{4}{3}$,
∴a=$\frac{5}{2}$,
在Rt△AMF中,∵tan∠FAM=$\frac{FM}{AM}$=$\frac{4}{3}$,AF=$\frac{5}{2}$,
∴FM=2.
点评 本题考查圆综合题、全等三角形的判定和性质、勾股定理、锐角三角函数、线段的垂直平分线的性质等知识,解题的关键是学会添加常用辅助线,灵活运用三角函数解决问题,属于中考压轴题.

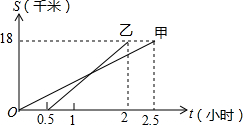 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )| A. | 乙比甲先到达B地 | B. | 乙在行驶过程中没有追上甲 | ||
| C. | 乙比甲早出发半小时 | D. | 甲的行驶速度比乙的行驶速度快 |
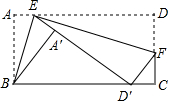 如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.
如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.