题目内容
12.如图,抛物线l:y=$\frac{1}{2}$(x-h)2-2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数?的图象.(1)若点A的坐标为(1,0).
①求抛物线l的表达式,并直接写出当x为何值时,函数?的值y随x的增大而增大;
②如图2,若过A点的直线交函数?的图象于另外两点P,Q,且S△ABQ=2S△ABP,求点P的坐标;
(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围.
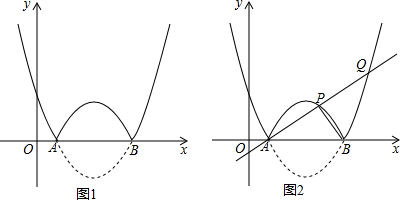
分析 (1)①利用待定系数法求抛物线的解析式,由对称性求点B的坐标,根据图象写出函数?的值y随x的增大而增大(即呈上升趋势)的x的取值;
②如图2,作辅助线,构建对称点F和直角角三角形AQE,根据S△ABQ=2S△ABP,得QE=2PD,证明△PAD∽△QAE,则$\frac{AE}{AD}=\frac{QE}{PD}$,得AE=2AD,设AD=a,根据QE=2FD列方程可求得a的值,并计算P的坐标;
(2)先令y=0求抛物线与x轴的两个交点坐标,根据图象中呈上升趋势的部分,有两部分:分别讨论,并列不等式或不等式组可得h的取值.
解答 解:(1)①把A(1,0)代入抛物线y=$\frac{1}{2}$(x-h)2-2中得:
$\frac{1}{2}$(x-h)2-2=0,
解得:h=3或h=-1,
∵点A在点B的左侧,
∴h>0,
∴h=3,
∴抛物线l的表达式为:y=$\frac{1}{2}$(x-3)2-2,
∴抛物线的对称轴是:直线x=3,
由对称性得:B(5,0),
由图象可知:当1<x<3或x>5时,函数?的值y随x的增大而增大;
②如图2,作PD⊥x轴于点D,延长PD交抛物线l于点F,作QE⊥x轴于E,则PD∥QE,
由对称性得:DF=PD,
∵S△ABQ=2S△ABP,
∴$\frac{1}{2}$AB•QE=2×$\frac{1}{2}$AB•PD,
∴QE=2PD,
∵PD∥QE,
∴△PAD∽△QAE,
∴$\frac{AE}{AD}=\frac{QE}{PD}$,
∴AE=2AD,
设AD=a,则OD=1+a,OE=1+2a,P(1+a,-[$\frac{1}{2}$(1+a-3)2-2]),
∵点F、Q在抛物线l上,
∴PD=DF=-[$\frac{1}{2}$(1+a-3)2-2],
QE=$\frac{1}{2}$(1+2a-3)2-2,
∴$\frac{1}{2}$(1+2a-3)2-2=-2[$\frac{1}{2}$(1+a-3)2-2],
解得:a=$\frac{8}{3}$或a=0(舍),
∴P($\frac{11}{3}$,$\frac{16}{9}$);
(2)当y=0时,$\frac{1}{2}$(x-h)2-2=0,
解得:x=h+2或h-2,
∵点A在点B的左侧,且h>0,
∴A(h-2,0),B(h+2,0),
如图3,作抛物线的对称轴交抛物线于点C,
分两种情况:
①由图象可知:图象f在AC段时,函数f的值随x的增大而增大,
则$\left\{\begin{array}{l}{h-2≤2}\\{h≥3}\end{array}\right.$,
∴3≤h≤4,
②由图象可知:图象f点B的右侧时,函数f的值随x的增大而增大,
即:h+2≤2,
h≤0,
综上所述,当3≤h≤4或h≤0时,函数f的值随x的增大而增大.
点评 本题是二次函数的综合题,考查了利用待定系数法求二次函数的解析式、二次函数的增减性问题、三角形相似的性质和判定,与方程相结合,找等量关系,第二问还运用了数形结合的思想解决问题.

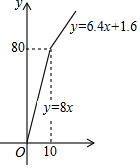 某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论:
某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论:(1)小明说:y与x之间的函数关系为y=6.4x+16
(2)小刚说:y与x之间的函数关系为y=8x
(3)小聪说:y与x之间的函数关系在0≤x≤10时,y=8x;在x>10时,y=6.4x+16
(4)小斌说:我认为用下面的列表法也能表示它们之间的关系
| 购买量/本 | 1 | 2 | 3 | 4 | … | 9 | 10 | 11 | 12 | … |
| 付款金额/元 | 8 | 16 | 24 | 32 | … | 72 | 80 | 86.4 | 92.8 | … |
其中,表示函数关系正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 4x2+10x+2 | B. | 10x-6 | C. | -10x+6 | D. | 6 |
 如图是七年级二班参加拓展性课程的扇形统计图,若参加唱歌的学生人数是12人,则参加绘画的学生有6人.
如图是七年级二班参加拓展性课程的扇形统计图,若参加唱歌的学生人数是12人,则参加绘画的学生有6人.