题目内容
9. 定义:如图,点P、Q把线段AB分割成线段AP、PQ和BQ,若以AP、PQ、BQ为边的三角形是一个直角三角形,则称点P、Q是线段AB的勾股分割点.已知点P、Q是线段AB的勾股分割点,如果AP=4,PQ=6(PQ>BQ),那么BQ=$2\sqrt{5}$.
定义:如图,点P、Q把线段AB分割成线段AP、PQ和BQ,若以AP、PQ、BQ为边的三角形是一个直角三角形,则称点P、Q是线段AB的勾股分割点.已知点P、Q是线段AB的勾股分割点,如果AP=4,PQ=6(PQ>BQ),那么BQ=$2\sqrt{5}$.
分析 由勾股定理求得BQ的长度即可.
解答 解:依题意得:AP2+BQ2=PQ2,即42+BQ2=62,
解得BQ=2$\sqrt{5}$(舍去负值).
故答案是:2$\sqrt{5}$.
点评 本题考查了勾股定理.熟知勾股分割点的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在△ABC中,∠A、∠B、∠C的对边长分别为a、b、c,且a2+c2=b2,则△ABC( )
| A. | ∠A为直角 | B. | ∠B为直角 | C. | ∠C为直角 | D. | 不是直角三角形 |
14.下列能和长度为3,4的两条线段组成锐角三角形的线段是( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
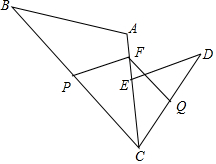 如图:E、A、C三点在同一条直线上,三角形ABC和三角形CDE是顶角相等的等腰三角形,其中BC和CD为等腰三角形的底边,F是AE的中点,P是BC边的中点,Q是CD边的中点.
如图:E、A、C三点在同一条直线上,三角形ABC和三角形CDE是顶角相等的等腰三角形,其中BC和CD为等腰三角形的底边,F是AE的中点,P是BC边的中点,Q是CD边的中点. 如图,△ABC的边BC=48cm.高AD=16cm,矩形EFGH的边FG在BC上,顶点E,H分别在AB、AC上,相邻两边EF,FG的比为5:9,求矩形EFGH的周长.
如图,△ABC的边BC=48cm.高AD=16cm,矩形EFGH的边FG在BC上,顶点E,H分别在AB、AC上,相邻两边EF,FG的比为5:9,求矩形EFGH的周长.