题目内容
分解因式:
(1)3(x+y)2-27;
(2)16x2-25y2;
(3)-x4+x2y2;
(4)16(x+y)2-25(x-y)2.
(1)3(x+y)2-27;
(2)16x2-25y2;
(3)-x4+x2y2;
(4)16(x+y)2-25(x-y)2.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)首先提取公因式3,进而利用平方差公式分解因式即可;
(2)直接利用平方差公式分解因式即可;
(3)首先提取公因式x2,进而利用平方差公式分解因式即可;
(4)直接利用平方差公式分解因式即可.
(2)直接利用平方差公式分解因式即可;
(3)首先提取公因式x2,进而利用平方差公式分解因式即可;
(4)直接利用平方差公式分解因式即可.
解答:解:(1)3(x+y)2-27
=3[(x+y)2-9]
=3(x+y-3)(x+y+3);
(2)16x2-25y2
=(4x-5y)(4x+5y);
(3)-x4+x2y2=x2(y2-x2)=x2(y-x)(y+x);
(4)16(x+y)2-25(x-y)2.
=[4(x+y)+5(x-y)][4(x+y)-5(x-y)]
=(9x-y)(-x+9y).
=3[(x+y)2-9]
=3(x+y-3)(x+y+3);
(2)16x2-25y2
=(4x-5y)(4x+5y);
(3)-x4+x2y2=x2(y2-x2)=x2(y-x)(y+x);
(4)16(x+y)2-25(x-y)2.
=[4(x+y)+5(x-y)][4(x+y)-5(x-y)]
=(9x-y)(-x+9y).
点评:此题主要考查了提取公因式法、公式法分解因式,熟练应用平方差公式是解题关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 有一张机械图纸上绘制了一个如图所示的弓形零件并有尺寸标注(单位:cm),工人师傅想要知道这个弓形的半径,请你帮他计算出来.
有一张机械图纸上绘制了一个如图所示的弓形零件并有尺寸标注(单位:cm),工人师傅想要知道这个弓形的半径,请你帮他计算出来. 如图,AB是⊙O直径,直线DC切⊙O于点C,过点B作BD⊥CD于点D,BD=3,AB=5,求BC.
如图,AB是⊙O直径,直线DC切⊙O于点C,过点B作BD⊥CD于点D,BD=3,AB=5,求BC.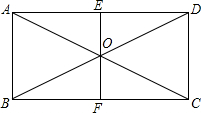 如图,点O为矩形ABCD对角线的交点,过点O作EF⊥BC于点F,若AB=2cm,BC=4cm,求四边形AECF的面积.
如图,点O为矩形ABCD对角线的交点,过点O作EF⊥BC于点F,若AB=2cm,BC=4cm,求四边形AECF的面积.