题目内容
16.等边三角形的内切圆半径为r,外接圆半径为R,高为h,则r:R:h的值为( )| A. | 1:2:3 | B. | 1:$\sqrt{3}$:2 | C. | 1:$\sqrt{2}$:2 | D. | 1:$\sqrt{2}$:$\sqrt{3}$ |
分析 根据等边三角形的内切圆和外接圆是同心圆,设圆心为O,根据30°角所对的直角边是斜边的一半得:R=2r;等边三角形的高是R与r的和,所以r:R:h的值为1:2:3.
解答 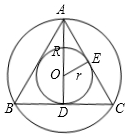 解:如图,∵△ABC是等边三角形,
解:如图,∵△ABC是等边三角形,
∴△ABC的内切圆和外接圆是同心圆,圆心为O,
设OE=r,AO=R,AD=h,
∵AD⊥BC,
∴∠DAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,
在Rt△AOE中,
∴R=2r,
OD=OE=r,
∴AD=AO+OD=2r+r=3r,
∴r:R:h=r:2r:3r=1:2:3,
故选A.
点评 本题考查了等边三角形及它的内切圆和外接圆的关系,等边三角形的内心与外心重合,是三条角平分线的交点;由等腰三角形三线合一的特殊性得出30°角和60°,利用直角三角形30°的性质或三角函数得出R、r、h的关系.

练习册系列答案
相关题目
6.如果a<3,那么|-2|+|a-4|等于( )
| A. | 6-a | B. | a-6 | C. | a-2 | D. | 2-a |
4.下列各式中,一定是二次根式的是( )
| A. | $\sqrt{a}$ | B. | $\sqrt{-10}$ | C. | $\sqrt{a+1}$ | D. | $\sqrt{{a}^{2}+1}$ |
11.在平面直角坐标中,将直线l1:y=2x平移后,得到直线l1:y=2x+6,则下列平移说法正确的是( )
| A. | 将l1向上平移6个单位长度 | B. | 将l1向下平移6个单位长度 | ||
| C. | 将l1向左平移6个单位长度 | D. | 将l1向右平移6个单位长度 |
 有理数x、y在数轴上对应的点的位置如图,化简|x-y+1|-2|y-x-3|+|y-x|+5.
有理数x、y在数轴上对应的点的位置如图,化简|x-y+1|-2|y-x-3|+|y-x|+5. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13.若P(m,2)在第13段抛物线C13上,则m的值为37或38.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13.若P(m,2)在第13段抛物线C13上,则m的值为37或38. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为3$\sqrt{2}$cm.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为3$\sqrt{2}$cm.