题目内容
 如图所示的圆锥底面半径OA=2cm,高PO=4
如图所示的圆锥底面半径OA=2cm,高PO=4| 2 |
考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:先根据勾股定理求出AP的长,再将圆锥的侧面展开,连接AA′,过点P作PD⊥AA′,根据弧长公式求出∠APA′的度数,进而可得出∠APD的度数,根据锐角三角函数的定义即可得出AD的长,进而结论.
解答: 解:如图所示:
解:如图所示:
∵OA=2cm,PO=4
cm,
∴AP=
=
=6cm,
=2π•2=4π,
设∠APA′=n°,则
=4π,解得n=120°,
∴∠APD=60°,
∴AD=AP•sin60°=6×
=3
cm,
∴AA′=2AD=6
cm.
故答案为:6
cm.
 解:如图所示:
解:如图所示:∵OA=2cm,PO=4
| 2 |
∴AP=
| OA2+OP2 |
22+(4
|
 |
| AA′ |
设∠APA′=n°,则
| nπ•6 |
| 180 |
∴∠APD=60°,
∴AD=AP•sin60°=6×
| ||
| 2 |
| 3 |
∴AA′=2AD=6
| 3 |
故答案为:6
| 3 |
点评:本题考查了平面展开-最短路线问题,弧长公式,勾股定理的应用,关键是能求出AD的长.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
二次函数y=2x2图象的顶点坐标是( )
| A、(0,0) |
| B、(1,1) |
| C、(1,0) |
| D、(0,1) |
计算x2•x3的结果是( )
| A、x6 |
| B、x2 |
| C、x3 |
| D、x5 |
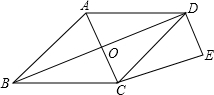 如图,已知平行四边形ABCD的对角线AC、BD交于点O,DE∥AC,CE∥BD,要使四边形OCED是矩形,则平行四边形ABCD还必须添加的条件是
如图,已知平行四边形ABCD的对角线AC、BD交于点O,DE∥AC,CE∥BD,要使四边形OCED是矩形,则平行四边形ABCD还必须添加的条件是 如图,已知Rt△ABC内切圆与斜边BC相切于点D,与直角边AB,AC分别相切于点E,F,则∠EDF=
如图,已知Rt△ABC内切圆与斜边BC相切于点D,与直角边AB,AC分别相切于点E,F,则∠EDF=