题目内容
已知△ABC是腰长为1的等腰直角三角形,以△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以△ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,依此类推,则△ABC 的面积为: ,第8个等腰直角三角形的面积是 .
考点:等腰直角三角形
专题:规律型
分析:根据△ABC是边长为1的等腰直角三角形分别求出Rt△ABC、Rt△ACD、Rt△ADE的面积,找出规律即可.
解答: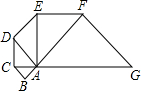 解:∵△ABC是边长为1的等腰直角三角形,
解:∵△ABC是边长为1的等腰直角三角形,
∴S△ABC=
×1×1═21-2;
AC=
=
,AD=
=2…,
∴S△ACD=
×
×
=1=22-2;
S△ADE=
×2×2=1=23-2…
∴第n个等腰直角三角形的面积是2n-2.
∴第8个等腰直角三角形的面积是28-2=64.
故答案为:
,64.
 解:∵△ABC是边长为1的等腰直角三角形,
解:∵△ABC是边长为1的等腰直角三角形,∴S△ABC=
| 1 |
| 2 |
AC=
| 12+12 |
| 2 |
(
|
∴S△ACD=
| 1 |
| 2 |
| 2 |
| 2 |
S△ADE=
| 1 |
| 2 |
∴第n个等腰直角三角形的面积是2n-2.
∴第8个等腰直角三角形的面积是28-2=64.
故答案为:
| 1 |
| 2 |
点评:本题考查的是等腰直角三角形,此题属规律性题目,答此题的关键是分别计算出图中所给的直角三角形的面积,找出规律.

练习册系列答案
相关题目
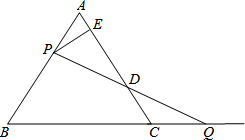 如图,△ABC是边长为12的等边三角形,P是AB上一动点,由A向B运动(与A、B点不重合),Q是BC延长线上一点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C点重合),过P作PE⊥AC于E,连接PQ交AC于D.
如图,△ABC是边长为12的等边三角形,P是AB上一动点,由A向B运动(与A、B点不重合),Q是BC延长线上一点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C点重合),过P作PE⊥AC于E,连接PQ交AC于D.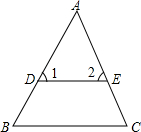 如图,在△ABC中,AB=AC,点D、E分别是AB、AC上的点,且DE∥BC,求证:△ADE是等腰三角形.
如图,在△ABC中,AB=AC,点D、E分别是AB、AC上的点,且DE∥BC,求证:△ADE是等腰三角形. 如图,已知∠DAC=∠BAC,那么添加一个条件
如图,已知∠DAC=∠BAC,那么添加一个条件 与三角形各边都相切的圆叫做三角形的
与三角形各边都相切的圆叫做三角形的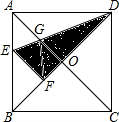 如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DEDE分别交ABAB、ACAC于点EE、GG连接GFGF,下列结论:
如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DEDE分别交ABAB、ACAC于点EE、GG连接GFGF,下列结论: 如图所示的圆锥底面半径OA=2cm,高PO=4
如图所示的圆锥底面半径OA=2cm,高PO=4