题目内容
抛物线y=2x2+4x-6与x轴的交点坐标是 ，与y轴的交点坐标是 ．
考点：抛物线与x轴的交点
专题：
分析：根据抛物线与x轴以及y轴交点坐标求法进而分别得出答案．
解答：解：抛物线y=2x2+4x-6与x轴相交时，y=0，
则0=2x2+4x-6，
解得：x1=1，x2=-3，
∴抛物线y=2x2+4x-6与x轴的交点坐标为：（1，0），（-3，0），
抛物线y=2x2+4x-6与y轴相交时，x=0，
则y=-6，
∴抛物线y=2x2+4x-6与y轴的交点坐标为：（0，-6），
故答案为：（1，0），（-3，0）；（0，-6）．
则0=2x2+4x-6，
解得：x1=1，x2=-3，
∴抛物线y=2x2+4x-6与x轴的交点坐标为：（1，0），（-3，0），
抛物线y=2x2+4x-6与y轴相交时，x=0，
则y=-6，
∴抛物线y=2x2+4x-6与y轴的交点坐标为：（0，-6），
故答案为：（1，0），（-3，0）；（0，-6）．
点评：此题主要考查了抛物线与坐标轴交点求法，正确解方程是解题关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
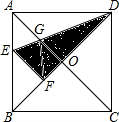如图，在正方形ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DEDE分别交ABAB、ACAC于点EE、GG连接GFGF，下列结论：
如图所示的圆锥底面半径OA=2cm，高PO=4
如图，若AC=DB，要证明△ABC≌△DCB，添加一个条件三角形中，到三边距离相等的点是（ ）
| A、三条高线的交点 |
| B、三条中线的交点 |
| C、三条角平分线的交点 |
| D、三边垂直平分线的交点 |