题目内容
8.计算:(-1)2015-($\frac{1}{3}$)-2+(2-$\sqrt{2}$)0-|-2|.分析 根据零指数幂、乘方、负整数指数幂、绝对值四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:原式=-1-9+1-2
=-11.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.

练习册系列答案
相关题目
19.在数轴上表示-2的点与表示3的点之间的距离是( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
16.在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.-2的倒数是( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
13.若一个几何体的主视图、左视图、俯视图都是正方形,则这个几何体是( )
| A. | 正方体 | B. | 圆锥 | C. | 圆柱 | D. | 球 |
5.下图是由边长为1的正方形按照某种规律排列而成.

(1)观察图形,填写下表:
(2)推测第n个图形中,正方形的个数为5n+3,周长为10n+8;
(3)根据上述规律排列,是否存在一个图形,它的周长为2014?

(1)观察图形,填写下表:
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
(3)根据上述规律排列,是否存在一个图形,它的周长为2014?
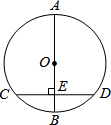 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=4-$\sqrt{7}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=4-$\sqrt{7}$.