��Ŀ����
4����һ�������ε����������㣺һ�ߵ����������ߵ�ƽ���������dz����������Ϊ��ƽ���������Ρ�����1�����и������ֱ��������ε������߳���
��5��7��5�� ��3��3��3�� ��6��8��4�� ��1��$\sqrt{3}$��2��
�����ܹ��ɡ�ƽ���������Ρ����Ǣڢۣ�����д��ţ�
��2����֪��ABC�������߳��ֱ�Ϊa��b��c����a��b��c������ABC���ǡ�ƽ���������Ρ�������ֱ�������Σ���$\frac{a}{b}$��ֵΪ$\frac{3}{4}$��
���� ��1������ƽ���������εĶ�����֤���ɵ�����𰸣�
��2���ɡ�ABC�ǡ�ƽ���������Ρ����ɵ�b=$\frac{a+c}{2}$������ֱ���������ɹ��ɶ����ɵã�a2+b2=c2�����������$\frac{a}{b}$��ֵ��
��� �⣺��1���ɡ�ƽ���������Ρ��ĸ����֪����3=$\frac{3+3}{2}$��������������6=$\frac{8+4}{2}$�����������������������⣬
�ʴ�Ϊ���ڢ�
��2���ߡ�ABC�ǡ�ƽ���������Ρ�����a��b��c��
��b=$\frac{a+c}{2}$�٣�
�ߡ�ABC��ֱ�������Σ�
��a2+b2=c2�ڣ�
�ɢ٢ڿ�֪��$\frac{a}{b}$=$\frac{3}{4}$��
�ʴ�Ϊ��$\frac{3}{4}$��
���� ���⿼���˹��ɶ����������Լ����¶�����Ŀ�Ľ�����п��������ͣ�������Ŀ�ѶȲ�����Ĺؼ�����ȷ������Ŀ�����ģ����¶��塱��

��ϰ��ϵ�д�
�����Ŀ
9��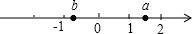 ʵ��a��b�������ϵ�λ����ͼ��ʾ����$\sqrt{��a-b��^{2}}$-$\sqrt{��1-a��^{2}}$-$\sqrt{{b}^{2}}$����ǣ�������
ʵ��a��b�������ϵ�λ����ͼ��ʾ����$\sqrt{��a-b��^{2}}$-$\sqrt{��1-a��^{2}}$-$\sqrt{{b}^{2}}$����ǣ�������
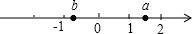 ʵ��a��b�������ϵ�λ����ͼ��ʾ����$\sqrt{��a-b��^{2}}$-$\sqrt{��1-a��^{2}}$-$\sqrt{{b}^{2}}$����ǣ�������
ʵ��a��b�������ϵ�λ����ͼ��ʾ����$\sqrt{��a-b��^{2}}$-$\sqrt{��1-a��^{2}}$-$\sqrt{{b}^{2}}$����ǣ�������| A�� | -2a-1 | B�� | -1 | C�� | 2b-1 | D�� | 1 |
16����$\sqrt{b}$=2��$\root{3}{a}$=-3����b-a��ֵ�ǣ�������
| A�� | 31 | B�� | -31 | C�� | 29 | D�� | -30 |
13����֪A��1��y1����B��2��y2����C��-3��y3�����ڷ���������y=$\frac{2}{x}$��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵ���ǣ�������
| A�� | y2��y1��y3 | B�� | y1��y2��y3 | C�� | y3��y2��y1 | D�� | y1��y3��y2 |
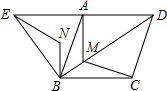 ��ͼ���ı���ABCD�����Σ��ҡ�ABC=60�㣬��ABE�ǵȱ������Σ�MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60��õ�BN������EN��AM��CM��
��ͼ���ı���ABCD�����Σ��ҡ�ABC=60�㣬��ABE�ǵȱ������Σ�MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60��õ�BN������EN��AM��CM��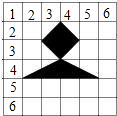 С������һ�ֽС������ڡ�����Ϸ�����С����������Ͷ����ͼ��ʾ��������ľ�壬��ô��������Ӱ���ֵĸ�����$\frac{1}{9}$��
С������һ�ֽС������ڡ�����Ϸ�����С����������Ͷ����ͼ��ʾ��������ľ�壬��ô��������Ӱ���ֵĸ�����$\frac{1}{9}$��