题目内容
18.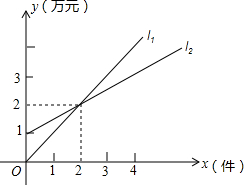 如图,L1表示某公司一种产品一天的销售收入与销售量的关系,L2表示该公司这种产品一天的销售成本与销售量的关系
如图,L1表示某公司一种产品一天的销售收入与销售量的关系,L2表示该公司这种产品一天的销售成本与销售量的关系(1)当x=1时,销售成本=$\frac{3}{2}$万元,盈利=-$\frac{1}{2}$万元;
(2)一天销售2件时,销售收入等于销售成本;
(3)L1对应的函数表达式是y=x;
(4)设利润为P万元,写出P与x的函数表达式.
分析 (1)根据线段中点的求法列式计算即可求出x=1时的销售收入和销售成本,根据盈利的求法计算即可得解;
(2)根据图象找出两直线的交点的横坐标即可;
(3)设l1对应的函数表达式为y=ax(k≠0),然后利用待定系数法求一次函数解析式解答;
(4)再写出l1的解析式,然后根据利润=销售收入-销售成本列式整理即可.
解答 解:(1)x=1时,销售成本=$\frac{1+2}{2}$=$\frac{3}{2}$万元,盈利(收入-成本)=1-$\frac{3}{2}$=-$\frac{1}{2}$万元;
(2)一天销售2件时,销售收入等于销售成本;
(3)设l1对应的函数表达式为:l1=ax,则2=2a,解得:a=1,
故l1对应的函数表达式为:l1=x;
(4)∵l1经过原点和(2,2),
∴l1的表达式为y=x,
∴利润p=x-($\frac{1}{2}$x+1)=$\frac{1}{2}$x-1.
故答案为:(1)$\frac{3}{2}$,-$\frac{1}{2}$;(2)2;(3)y=x.
点评 本题考查了一次函数的应用,考查了识别函数图象的能力,待定系数法求一次函数解析式,准确观察图象提供的信息是解题的关键.

练习册系列答案
相关题目
8.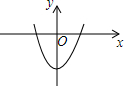 已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
 已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法判断 |
9.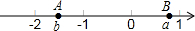 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
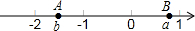 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
6.关于函数y=8x-m(m不等于0),下列结论正确的是( )
| A. | 函数图象一定经过第一、三 | B. | 函数图象经过点(0,0) | ||
| C. | y随x的增大而减小 | D. | 不论x取何值,总有y大于0 |
10. 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )| A. | $\sqrt{23}$ | B. | $\sqrt{13}$ | C. | $\sqrt{17}$ | D. | $\sqrt{26}$ |
 如图,?ABCD的周长为50,其中AB=12,∠ABC=60°,求?ABCD的面积.
如图,?ABCD的周长为50,其中AB=12,∠ABC=60°,求?ABCD的面积.