题目内容
8.如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.可证:AE⊥BF;(1)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM,如图2,若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
(2)将△BCF沿BF对折,得到△BPF,如图3,延长FP交BA的延长线于点Q,求sin∠BQP的值;
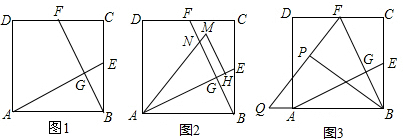
分析 (1)先求出正方形的边长,再根据面积比等于相似边长比的平方,求得S△AGN=$\frac{4}{5}$,再利用S四边形GHMN=S△AHM-S△AGN求解;
(2)△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,解出BP,QB求解.
解答 解:(1)∵正方形ABCD的面积为4,其边长为2,由题意得:
∵∠BAE=∠EAM,AE⊥BF,
∴AN=AB=2,
∵∠AHM=90°,
∴GN∥HM,
∴△AGN∽△AHM,
∴$\frac{{S}_{△AGN}}{{S}_{△AHM}}=(\frac{AN}{AM})^{2}$,
∴$\frac{{S}_{△AGN}}{1}=(\frac{2}{\sqrt{5}})^{2}$,
∴S△AGN=$\frac{4}{5}$,
∴S四边形GHMN=S△AHM-S△AGN=1-$\frac{4}{5}$=$\frac{1}{5}$,
∴四边形GHMN的面积是$\frac{1}{5}$.
(2)根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
令PF=k(k>0),则PB=2k
在Rt△BPQ中,设QB=x,
∴x2=(x-k)2+4k2,
∴x=$\frac{5k}{2}$,
∴sin=∠BQP=$\frac{BP}{QB}=\frac{2k}{\frac{5k}{2}}=\frac{4}{5}$.
点评 本题主要考查了四边形的综合题,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
3.某组同学分发一批数学练习本,如果每人分5本,则多5本;如果每人分6本,则少6本,假设有x个同学,y本数学练习本,则正确的方程组是( )
| A. | $\left\{\begin{array}{l}{y=5x+5}\\{y-6=6x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y+5=5x}\\{y=6x-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+5=5x}\\{y=6x+6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=5x+5}\\{y+6=6x}\end{array}\right.$ |
13.某校运动员分组训练,若每组6人,余3人;若每组7人,则缺5人;设运动员人数为x 人,组数为y组,则列方程组为( )
| A. | $\left\{\begin{array}{l}{6y=x+3}\\{7y=x+5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6y=x-3}\\{7y+5=x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{6y=x+3}\\{7y+5=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6y=x-3}\\{7y=x+5}\end{array}\right.$ |
20.己知关于x的方程(a2-1)x2+(1-a)x+a-2=0,下列结论正确的是( )
| A. | 当a≠±1时,原方程是一元二次方程 | B. | 当a≠1时,原方程是一元二次方程 | ||
| C. | 当a≠-1时,原方程是一元二次方程 | D. | 原方程是一元二次方程 |
 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的2块带去,就能配一块大小和形状与原来都一样的三角形.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的2块带去,就能配一块大小和形状与原来都一样的三角形.