题目内容
9.先化简再求值:$\frac{3x-3}{{x}^{2}-1}$÷$\frac{3x}{x+1}$-$\frac{1}{x-1}$,并选一个你喜欢的数代入求值.分析 先把分子分母因式分解和除法运算化为乘法运算,约分后进行通分得到原式=-$\frac{1}{{x}^{2}-x}$,由于x不能取0,±1,可把x=10代入计算即可.
解答 解:原式=$\frac{3(x-1)}{(x+1)(x-1)}$•$\frac{x+1}{3x}$-$\frac{1}{x-1}$
=$\frac{1}{x}$-$\frac{1}{x-1}$
=$\frac{x-1-x}{x(x-1)}$
=-$\frac{1}{{x}^{2}-x}$,
当x=10时,原式=-$\frac{1}{100-10}$=-$\frac{1}{90}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
20. 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 3:4 |
4.细胞分裂按照一分为二,二分为四,四分为八…,如此规律进行,例如1个细胞分裂10次可以得到细胞的个数为210=1024个,估计1个细胞分裂40次所得细胞的个数为( )
| A. | 七位数 | B. | 十二位数 | C. | 十三位数 | D. | 十四位数 |
1. 一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
 一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )| A. | 步 | B. | 量 | C. | 青 | D. | 春 |
 如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为( )
如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为( )
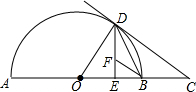 如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.
如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.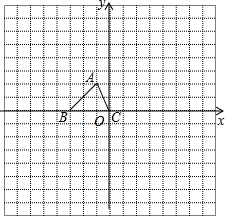 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).
如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).