题目内容
12.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )| A. | 56 | B. | 48 | C. | 40 | D. | 32 |
分析 根据题意画出图形,进而利用勾股定理得出DC的长,进而求出BC的长,即可得出答案.
解答  解:过点A做AD⊥BC于点D,
解:过点A做AD⊥BC于点D,
∵等腰三角形底边上的高为8,周长为32,
∴AD=8,设DC=BD=x,则AB=$\frac{1}{2}$(32-2x)=16-x,
∴AC2=AD2+DC2,即(16-x)2=82+x2,
解得:x=6,
故BC=12,
则△ABC的面积为:$\frac{1}{2}$×AD×BC=$\frac{1}{2}$×8×12=48.
故选:B.
点评 此题主要考查了勾股定理以及等腰三角形的性质,得出DC的长是解题关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{14}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{4}$ |
 如图,已知△ABC中,高为AD,角平分线为AE,若∠B=28°,∠ACD=52°,求∠EAD的度数.
如图,已知△ABC中,高为AD,角平分线为AE,若∠B=28°,∠ACD=52°,求∠EAD的度数.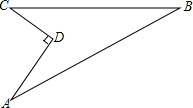 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?