题目内容
2.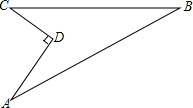 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?
分析 连接AC,先利用勾股定理求出AC,再根据勾股定理的逆定理判定△ABC是直角三角形,那么△ABC的面积减去△ACD的面积就是所求的面积.
解答 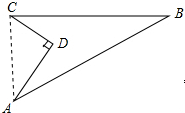 解:如图,连接AC.
解:如图,连接AC.
在△ACD中,∵AD=4米,CD=3米,∠ADC=90°,
∴AC=5米,
又∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴这块地的面积=△ABC的面积-△ACD的面积=$\frac{1}{2}$×5×12-$\frac{1}{2}$×3×4=24(平方米).
点评 本题考查了勾股定理、勾股定理的逆定理的应用,得到△ABC是直角三角形是解题的关键.同时考查了直角三角形的面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
| A. | 56 | B. | 48 | C. | 40 | D. | 32 |
17.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{45}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{5{a}^{2}}$ | D. | $\sqrt{7}$ |
7.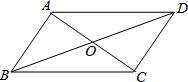 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )| A. | ∠BAD=∠BCD,∠ABC=∠ADC | B. | OA=OC,OB=OD | ||
| C. | AD∥BC,AB=CD | D. | AC=BD,AD=CD |
14.抛物线y=(x+4)2+3的顶点坐标是( )
| A. | (4,-3) | B. | (-4,-3) | C. | (4,3) | D. | (-4,3) |