题目内容
1.先观察:1-$\frac{1}{{2}^{2}}$=$\frac{1}{2}$×$\frac{3}{2}$,1-$\frac{1}{{3}^{2}}$=$\frac{2}{3}$×$\frac{4}{3}$,1-$\frac{1}{{4}^{2}}$=$\frac{3}{4}$×$\frac{5}{4}$,…(1)探究规律填空:1-$\frac{1}{{n}^{2}}$=$\frac{n-1}{n}$×$\frac{n+1}{n}$;
(2)计算:(1-$\frac{1}{{2}^{2}}$)$•(1-\frac{1}{{3}^{2}})$$•(1-\frac{1}{{4}^{2}})$…(1-$\frac{1}{201{0}^{2}}$)
分析 (1)原式利用平方差公式变形,计算即可得到结果;
(2)原式利用平方差公式变形,结合后,约分即可得到结果.
解答 解:(1)1-$\frac{1}{{n}^{2}}$=(1+$\frac{1}{n}$)(1-$\frac{1}{n}$)=$\frac{n+1}{n}$×$\frac{n-1}{n}$;
故答案为:$\frac{n+1}{n}$;$\frac{n-1}{n}$;
(2)原式=(1+$\frac{1}{2}$)(1-$\frac{1}{2}$)(1+$\frac{1}{3}$)(1-$\frac{1}{3}$)…(1+$\frac{1}{2010}$)(1-$\frac{1}{2010}$)=$\frac{3}{2}$×$\frac{4}{3}$×…×$\frac{2011}{2010}$×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{2009}{2010}$=$\frac{2011}{2}$×$\frac{1}{2010}$=$\frac{2011}{4020}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
12.下列方程的解是x=2的是( )
| A. | x-$\frac{1}{2}$=0 | B. | 6x-12=0 | C. | -4x+6=0 | D. | 2x+4=0 |
4.方程2(x+3)(x-4)=x2-10的一般形式为( )
| A. | x2-2x-14=0 | B. | x2+2x+14=0 | C. | x2+2x-14=0 | D. | x2-2x+14=0 |
8. 如图,在⊙O中,弦的条数是( )
如图,在⊙O中,弦的条数是( )
 如图,在⊙O中,弦的条数是( )
如图,在⊙O中,弦的条数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 以上均不正确 |
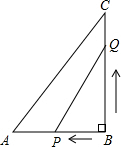 如图,在△ABC中,∠B=90°,AB=8cm,BC=12cm,点P从B点开始沿BA边向A以1cm/s的速度移动,点Q也从B点开始沿BC边向点C以2cm/s的速度移动,设运动时间为t秒.
如图,在△ABC中,∠B=90°,AB=8cm,BC=12cm,点P从B点开始沿BA边向A以1cm/s的速度移动,点Q也从B点开始沿BC边向点C以2cm/s的速度移动,设运动时间为t秒.