题目内容
 如图,已知AB为⊙O的弦,OD⊥AB于点C,DA与⊙O相切于点A,若AB=8cm,其弦心距等于3cm,则DA=
如图,已知AB为⊙O的弦,OD⊥AB于点C,DA与⊙O相切于点A,若AB=8cm,其弦心距等于3cm,则DA=考点:垂径定理,相似三角形的判定与性质
专题:
分析:先根据垂径定理求出AC的长,再根据相似三角形的判定定理得出△AOC∽△COD,再由相似三角形的对应边成比例即可得出结论.
解答:解:∵AB为⊙O的弦,OD⊥AB于点C,AB=8cm,
∴AC=
AB=4cm,∠ACO=90°.
∵OC=3cm,
∴AO=
=
=5.
∵DA与⊙O相切于点A,
∴∠OAD=90°,
∴△AOC∽△COD,
∴
=
,即
=
,解得DA=
(cm).
故答案为:
cm.
∴AC=
| 1 |
| 2 |
∵OC=3cm,
∴AO=
| AC2+OC2 |
| 42+32 |
∵DA与⊙O相切于点A,
∴∠OAD=90°,
∴△AOC∽△COD,
∴
| OC |
| OA |
| AC |
| DA |
| 3 |
| 5 |
| 4 |
| DA |
| 20 |
| 3 |
故答案为:
| 20 |
| 3 |
点评:本题考查的是垂径定理,熟知垂直于弦的直径平分弦是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
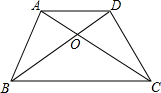 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,S△AOD:S△DOC=4:9,则
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,S△AOD:S△DOC=4:9,则| AD |
| BC |
| A、2:3 | B、4:9 |
| C、4:13 | D、4:5 |
如果a=
+
,b=
,那么a与b的关系式( )
| 6 |
| 5 |
| 1 | ||||
|
| A、a与b互为相反数 |
| B、a与b互为倒数 |
| C、a>b |
| D、a=b |
 如图所示,在平面直角坐标系第二象限中,△ABO的顶点B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°.
如图所示,在平面直角坐标系第二象限中,△ABO的顶点B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°. 如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2=
如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2=