题目内容
设a,b是正整数,满足ab-a+3b=63,那么a+2b的最小值是 .
考点:多元函数的最值
专题:
分析:根据ab-a+3b=63进行因式分解,得到(a+3)(b-1)=60,得出b不等于1,即可求出a的值,再根据基本不等式的性质即可求出a+2b的最小值.
解答:解:由ab-a+3b=63,进行因式分解整理得:(a+3)(b-1)=60,
所以b-1≠0,则a=
-3,
则a+2b=
-3+2b=
+2(b-1)-1≥2
-1=2
-1=4
-1,
∵a,b是正整数,
∴a+2b最小值为:21,
故答案为:21.
所以b-1≠0,则a=
| 60 |
| b-1 |
则a+2b=
| 60 |
| b-1 |
| 60 |
| b-1 |
|
| 120 |
| 30 |
∵a,b是正整数,
∴a+2b最小值为:21,
故答案为:21.
点评:此题考查了多元函数的最值,解题的关键是对要求的式子进行分解,再利用基本不等式的性质求出最值.

练习册系列答案
相关题目
下列图案中,既是中心对称又是轴对称的图案是( )
A、 |
B、 |
C、 |
D、 |
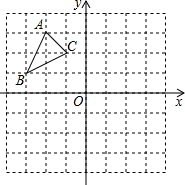 如图,△ABC中A(-2,3),B(-3,1),C(-1,2).
如图,△ABC中A(-2,3),B(-3,1),C(-1,2).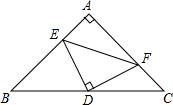 如图,在等腰Rt△ABC中,D是斜边BC的中点,E在边AB上,F在边AC上,且∠EDF=90°.
如图,在等腰Rt△ABC中,D是斜边BC的中点,E在边AB上,F在边AC上,且∠EDF=90°.