题目内容
15.对于函数y=(k-1)x2-4x+5-k,下列说法正确的是( )| A. | 不论k为何值,图象一定经过(1,0)和(-1,0) | |
| B. | 不论k为何值,函数一定有最大值或最小值 | |
| C. | 当x≤1时 y随x的增大而增大,则k的取值范围是k≤3 | |
| D. | 不论k为何值,图象与x轴一定有公共点 |
分析 A、令k=1时,得到函数y=-4x+4,根据函数的解析式即可判断;
B、令k=1时,得到函数y=-4x+4,根据直线没有最大值,也没有最小值即可判断;
C、当x≤1时 y随x的增大而增大,则x=-$\frac{-4}{k-1}$≥1,且k-1<0,解不等式即可判断;
D、计算出△,根据△的值进行判断;
解答 解:A、令k=1时,函数y=-4x+4,则函数图象经过(1,0),不经过(-1,0),故错误;
B、令k=1时,函数y=-4x+4,则函数的图象是一条直线,函数没有最大值,也没有最小值,故错误;
C、当x≤1时 y随x的增大而增大,则x=-$\frac{-4}{k-1}$≥1,且k-1<0,
解-$\frac{-4}{k-1}$≥1,得k≥5,故错误;
D、b2-4ac=(-4)2-4(k-1)(5-k)=4(k-3)2≥0,所以图象与x轴一定有公共点,故正确.
故选D.
点评 本题考查了二次函数的性质,一次函数的性质,熟悉函数和函数方程的关系、函数的性质是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
3.湘湖二期是第二届世界休闲博览会的主园区,建成了52座景观桥梁;实施了105万平方米沿湖景观绿化,同时还建设开幕式会场、休闲大舞台、音乐喷泉、美食街、大型停车场等休博会配套设施.105万平方米用科学记数法表示应记为( )平方米.
| A. | 1.05×102 | B. | 1.05×104 | C. | 1.05×105 | D. | 1.05×106 |
20.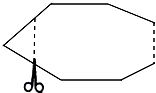 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )| A. | 77 | B. | 90 | C. | 65 | D. | 104 |
7.在算式$\sqrt{2011}$×$\sqrt{2012}$×$\sqrt{2013}$×$\sqrt{2014}$中,你估计哪一个因数值减小1导致乘积减小最大( )
| A. | $\sqrt{2011}$ | B. | $\sqrt{2012}$ | C. | $\sqrt{2013}$ | D. | $\sqrt{2014}$ |
5.下列方程:①x-2y=5;②6x+y2=5;③3x+1=y;④y=9中,是二元一次方程的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
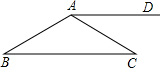 如图,在△ABC中,AB=AC,AD∥BC,∠BAC=130°,则∠DAC等于25°.
如图,在△ABC中,AB=AC,AD∥BC,∠BAC=130°,则∠DAC等于25°.