题目内容
6．
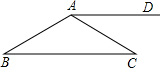如图，在△ABC中，AB=AC，AD∥BC，∠BAC=130°，则∠DAC等于25°．
分析 由等腰三角形的性质可求得∠C，再根据平行线的性质可求得∠DAC．
解答 解：∵AB=AC，
∴∠B=∠C，
∴∠BAC=130°，
∴∠C=$\frac{180°-130°}{2}$=25°，
∵AD∥BC，
∴∠DAC=∠C=25°，
故答案为：25．
点评 本题主要考查等腰三角形的性质和平行线的性质，根据等腰三角形的两底角相等求得∠C的度数是解题的关键．
练习册系列答案
相关题目
17．下列函数中，自变量x的取值范围是x≥1的是（ ）
| A． | y=$\frac{1}{x-1}$ | B． | y=$\frac{1}{\sqrt{x-1}}$ | C． | y=$\sqrt{x-1}$ | D． | y=x-1 |
1．分式$\frac{1}{1-x}$有意义的条件是（ ）
| A． | x≠1 | B． | x＞0 | C． | x≠-1 | D． | x＜0 |
如图，直线a∥b∥c，点A、B、C分别在直线a、b、c上，若∠1=70°，∠2=50°，则∠ABC=120．
15．对于函数y=（k-1）x2-4x+5-k，下列说法正确的是（ ）
| A． | 不论k为何值，图象一定经过（1，0）和（-1，0） | |
| B． | 不论k为何值，函数一定有最大值或最小值 | |
| C． | 当x≤1时 y随x的增大而增大，则k的取值范围是k≤3 | |
| D． | 不论k为何值，图象与x轴一定有公共点 |
如图，AD平分∠BAC，AB=AC，那么△ABD≌△ACD吗？请说明理由．