题目内容
如图，在△ABD和△AEC中，已知BD=CE，∠BEC=∠CDB，求证：AB=AC．考点：全等三角形的判定与性质
专题：证明题
分析：利用∠BEC=∠CDB得到∠ADB=∠AEC，然后根据三角全等的判定方法AAS可得到△ADB≌△AEC，则根据全等的性质即可得到AB=AC．
解答：解：∵∠BEC=∠CDB
∴∠ADB=∠AEC
在△ADB和△AEC中，
，
∴△ADB≌△AEC（AAS），
∴AB=AC．
∴∠ADB=∠AEC
在△ADB和△AEC中，
|
∴△ADB≌△AEC（AAS），
∴AB=AC．
点评：本题考查了全等三角形的判定与性质：有两组角分别相等，且其中一组角所对的边对应相等，那么这两个三角形全等；全等三角形的对应边相等，对应角相等．
练习册系列答案
相关题目
把一副三角板按如图叠放在一起，则∠α的度数是（ ）| A、165° | B、160° |
| C、155° | D、150° |
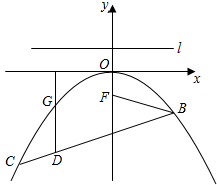如图，抛物线y=ax2+bx+c关于y轴对称，它的顶点在坐标原点O，点B（2，-
在平面直角坐标系xOy中，等腰△OAD的底边OA在x轴上，顶点D（2，-4a）（a≠0），抛物线y=a2+bx+c经过O，A，D三点．