题目内容
14.下列四组数:①32,42,52;②0.5,1.2,1.3;③8,15,17;④7,24,25,其中是勾股数的有( )| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
分析 欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
解答 解:①(32)2+(42)2≠(52 ),不是勾股数;
②0.52+1.22=1.32,三边不是整数,能构成直角三角形,不是勾股数;
③82+152=172,三边是整数,同时能构成直角三角形,是勾股数;
④72+242=252,且7,24,25都是正整数,同时能构成直角三角形,是勾股数,
故选:C.
点评 此题主要考查了勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6. 如图,已知EA∥DF,AE=DF,要使△AEC≌△DBF,则需要( )
如图,已知EA∥DF,AE=DF,要使△AEC≌△DBF,则需要( )
 如图,已知EA∥DF,AE=DF,要使△AEC≌△DBF,则需要( )
如图,已知EA∥DF,AE=DF,要使△AEC≌△DBF,则需要( )| A. | AB=CD | B. | EC=BF | C. | ∠A=∠D | D. | AB=BC |
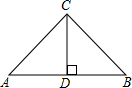 在△ABC中,AC=BC,∠ACB=90°,CD⊥AB于D,若S△ABC=16,则CD=4.
在△ABC中,AC=BC,∠ACB=90°,CD⊥AB于D,若S△ABC=16,则CD=4. 如图,阴影部分是3个直角三角形,若最大正方形的边长为16,则正方形A,B,C,D的面积和是256.
如图,阴影部分是3个直角三角形,若最大正方形的边长为16,则正方形A,B,C,D的面积和是256.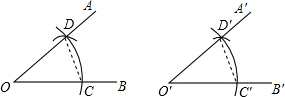 如图,用直尺和圆规作一个角等于已知角,能得出的依据是SSS.
如图,用直尺和圆规作一个角等于已知角,能得出的依据是SSS.