题目内容
9.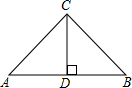 在△ABC中,AC=BC,∠ACB=90°,CD⊥AB于D,若S△ABC=16,则CD=4.
在△ABC中,AC=BC,∠ACB=90°,CD⊥AB于D,若S△ABC=16,则CD=4.
分析 根据AC=BC,∠ACB=90°,于是判断△ABC是等腰直角三角形,由于CD⊥AB于D,根据等腰直角三角形的性质得到CD=$\frac{1}{2}$AB,然后根据面积公式列方程即可得到结果.
解答 解:∵AC=BC,∠ACB=90°,
∴△ABC是等腰直角三角形,
∵CD⊥AB于D,
∴CD=$\frac{1}{2}$AB,
∴S△ABC=$\frac{1}{2}$AB•CD=CD2=16,
∴CD=4(负值舍去).
故答案为:4.
点评 本题考查了等腰直角三角形的性质,三角形的面积公式,熟练掌握等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
4.“$\frac{36}{25}$的平方根是±$\frac{6}{5}$”用数学式表示为( )
| A. | $\sqrt{\frac{36}{25}}$=$±\frac{6}{5}$ | B. | $±\sqrt{\frac{36}{25}}$=$±\frac{6}{5}$ | C. | $\sqrt{\frac{36}{25}}$=$\frac{6}{5}$ | D. | -$\sqrt{\frac{36}{25}}$=-$\frac{6}{5}$ |
14.下列四组数:①32,42,52;②0.5,1.2,1.3;③8,15,17;④7,24,25,其中是勾股数的有( )
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
19.一次课堂练习,小颖同学做了如下4道因式分解题,你认为小颖做的不够完整的一道题是( )
| A. | x3-4x2+4x=x(x2+4x+4) | B. | x2y-xy2=xy(x-y) | ||
| C. | x2-y2=(x-y)(x+y) | D. | x2-2xy+y2=(x-y)2 |
 如图所示,将两条等宽的纸条重叠在一起,则四边形ABCD是菱形.
如图所示,将两条等宽的纸条重叠在一起,则四边形ABCD是菱形.
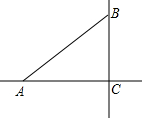 如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为20°或40°或70°或100°.
如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为20°或40°或70°或100°.