题目内容
18.在锐角三角形ABC中,AC=100,tanA=1,tanC=2,求BC的长和△ABC的面积.分析 根据题意可以画出相应的图形,由在锐角三角形ABC中,AC=100,tanA=1,tanC=2,可以求得AC的长,从而可以求得BC的长和△ABC的面积.
解答 解:根据题意,如下图所示: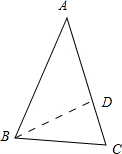
作BD⊥AC于点D,则∠BDA=∠BDC=90°,
∵tanA=1,tanC=2,tanA=$\frac{BD}{AD}$,tanC=$\frac{BD}{CD}$,AC=AD+CD,AC=100,
∴BD=AD,BD=2CD.
∴AD+CD=3CD=AC=100.
∴CD=$\frac{100}{3}$,AD=$\frac{200}{3}$,BD=$\frac{200}{3}$,BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\frac{100\sqrt{5}}{3}$.
∴${S}_{△ABC}=\frac{AC×BD}{2}=\frac{100×\frac{200}{3}}{2}=\frac{10000}{3}$.
即BC的长为$\frac{100\sqrt{5}}{3}$,△ABC的面积是$\frac{10000}{3}$.
点评 本题考查解直角三角形,解题的关键是画出相应的图形,找出所求问题需要的条件.

练习册系列答案
相关题目
3.下列说法错误的是( )
| A. | 一个四边形最多有三个锐角 | B. | 一个四边形最多有三个直角 | ||
| C. | 一个四边形最多有三个钝角 | D. | 一个四边形可能有一个锐角 |
8.解方程$\frac{2x-1}{3}$-$\frac{3x-4}{12}$=1,下列变形正确的是( )
| A. | 4(2x-1)-(3x-4)=1 | B. | 4(2x-1)-3x-4=12 | C. | 4(2x-1)-(3x-4)=4 | D. | 4(2x-1)-3x+4=12 |