��Ŀ����
16����ͼ��ʾ��AB��CD��ֱ��EF��AB�ཻ�ڵ�E����CD�ཻ�ڵ�F��FH�ǡ�EFD�Ľ�ƽ���ߣ�����AB�ཻ�ڵ�H��GF��FH��AB�ڵ�G��GF��HP������1����ͼ�٣���֤����E��GH���е㣻
��2����ͼ�ڣ�����E��EP��AB��GF�ڵ�P�����ж�GP2=PF2+HF2�Ƿ��������˵�����ɣ�
��3����ͼ�ۣ��ڣ�1���������£�����E��EP��EF��GF�ڵ�P��������߶�GP��PF��HF��������������ϵ����ֱ��д�������Ľ����

���� ��1������ƽ���ߵ����ʺͽ�ƽ���ߵĶ�����á�EHF=��EFH��֤��EF=EH�����ݡ�EFG+��EFH=90�㣬��EGF+��EHF=90�㣬�ó���EFG=��EGF�����ݵȽǶԵȱ����EG=EF������֤��EH=EG����EΪHG���е㣻
��2������PH�����ݴ�ֱƽ���ߵ����ʵó�PG=PH����Rt��PFH�У����ݹ��ɶ����ã�PH2=PF2+HF2�����ɵõ�GP2=PF2+HF2��
��3���ӳ�PE��ʹPE=EM������MH��MF����֤�á�GPE�ա�HME���Ӷ��ó�GP=MH����1=��2������֤��EF��ֱƽ��PM�����ݴ�ֱƽ���ߵ����ʵó�PF=MF����RT��MHF�У�MF2=MH2+FH2�����ɵõ�PF2=GP2+FH2��
��� ��1��֤������AB��CD��
���EHF=��HFD��
��FHƽ�֡�EFD��
���EFH=��HFD��
���EHF=��EFH��
��EF=EH��
�ߡ�GFH=90�㣬
���EFG+��EFH=90�㣬��EGF+��EHF=90�㣬
���EFG=��EGF��
��EG=EF��
��EH=EG��
��EΪHG���е㣻
��2������PH����ͼ��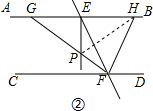 ��
��
��EP��AB��
�֡�E��GH�е㣬
��PE��ֱƽ��GH��
��PG=PH��
��Rt��PFH�У���PFH=90�㣬
�ɹ��ɶ����ã�PH2=PF2+HF2��
��GP2=PF2+HF2�� 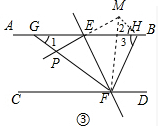
��3����ͼ�ۣ��ӳ�PE��ʹPE=EM������MH��MF��
�ڡ�GPE�͡�HME�У�
$\left\{\begin{array}{l}{GE=EH}\\{��GEP=��HEM}\\{PE=EM}\end{array}\right.$��
���GPE�ա�HME��SAS����
��GP=MH����1=��2��
��GF��FH��
���1+��3=90�㣬
���2+��3=90�㣬
��EF��PM��PE=EM��
��PF=MF��
��RT��MHF��MF2=MH2+FH2��
��PF2=GP2+FH2��
���� ���⿼����ȫ�������ε��ж������ʣ��߶εĴ�ֱƽ���ߵ����ʣ����������ε��ж������ʣ����ɶ�����Ӧ�õȣ��ҳ������ߣ����������������ǽ���Ĺؼ���

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�| A�� | 0 | B�� | 3 | C�� | -3 | D�� | ������ |
| A�� | ӯ��$\frac{25}{9}$Ԫ | B�� | ����10Ԫ | C�� | ӯ��15Ԫ | D�� | ��Ӯ���� |
 ��ͼ��һ��������a���ѳ�����������b��һ��������b�ַ��ѳ�����������c��һ��������c�з��ѳ�����������d�������������ƣ���������f�ĸ�����25��������ݵ���ʽ��ʾ����
��ͼ��һ��������a���ѳ�����������b��һ��������b�ַ��ѳ�����������c��һ��������c�з��ѳ�����������d�������������ƣ���������f�ĸ�����25��������ݵ���ʽ��ʾ����


 ijƷ�Ƽ���������ڼ�����涨ÿ̨������ۼ�0.7��Ԫ���״θ����ÿ����Ӧ����Ǯ��y��Ԫ���뻹Ǯ����t�Ĺ�ϵ��ͼ��ʾ��
ijƷ�Ƽ���������ڼ�����涨ÿ̨������ۼ�0.7��Ԫ���״θ����ÿ����Ӧ����Ǯ��y��Ԫ���뻹Ǯ����t�Ĺ�ϵ��ͼ��ʾ��