��Ŀ����
1����ͼ1���ڡ�ABC�У�BC=4�����߶�ABΪ������ABD��ʹ��AD=BD������DC������DCΪ������CDE��ʹ��DC=DE����CDE=��ADB=������1����ͼ2������ABC=45���Ҧ�=90��ʱ���õ�ʽ��ʾ�߶�AD��DE֮���������ϵ��
��2�����߶�CB��������CE�ķ���ƽ�ƣ��õ��߶�EF������BF��AF��
������=90�㣬�����ⲹȫͼ3�����߶�AF�ij���
����ֱ��д���߶�AF�ij����ú�����ʽ�ӱ�ʾ����

���� ��1�����ݵ���ֱ�������ε����ʵó����ɣ�
��2������DE��BC�ཻ�ڵ�H������ AE����BC�ڵ�G������SAS�Ƴ���ADE�ա�BDC������ȫ�������ε����ʵó�AE=BC����AED=��BCD�������AFE=45�㣬��ֱ��������������ɣ�
�ڹ�E��EM��AF��M�����ݵ��������ε����ʵó���AEM=��FEM=$\frac{��}{2}$��AM=FM����ֱ�����������FM���ɣ�
��� �⣺��1��AD+DE=4��
�����ǣ���ͼ1��
�ߡ�ADB=��EDC=�Ϧ�=90�㣬AD=BD��DC=DE��
��AD+DE=BC=4��
��2���ٲ�ȫͼ�Σ���ͼ2��
��DE��BC�ཻ�ڵ�H������AE��
��BC�ڵ�G��
�ߡ�ADB=��CDE=90�㣬
���ADE=��BDC��
�ڡ�ADE���BDC�У�
$\left\{\begin{array}{l}AD=BD\\��ADE=��BDC\\ DE=DC\end{array}\right.$��
���ADE�ա�BDC��
��AE=BC����AED=��BCD��
��DE��BC�ཻ�ڵ�H��
���GHE=��DHC��
���EGH=��EDC=90�㣬
���߶�CB��������CE�ķ���ƽ�ƣ��õ��߶�EF��
��EF=CB=4��EF��CB��
��AE=EF��
��CB��EF��
���AEF=��EGH=90�㣬
��AE=EF����AEF=90�㣬
���AFE=45�㣬
��AF=$\frac{EF}{{cos{{45}��}}}$=4$\sqrt{2}$��
����ͼ2����E��EM��AF��M��
���ɢ�֪��AE=EF=BC��
���AEM=��FEM=$\frac{��}{2}$��AM=FM��
��AF=2FM=EF��sin$\frac{��}{2}$=8sin$\frac{��}{2}$��
���� ���⿼����ȫ�������ε����ʺ��ж�����ֱ�������Σ����������ε����ʣ�ƽ�Ƶ����ʵ�Ӧ�ã�����ȷ�����������ǽ����Ĺؼ����ۺ��ԱȽ�ǿ���Ѷ�ƫ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� ��ͼ����֪��AB=CD��AD=BC
��ͼ����֪��AB=CD��AD=BC ��ͼ����֪AB=CD��BE=DF��AF=CE����֤����ABE=��CDF��
��ͼ����֪AB=CD��BE=DF��AF=CE����֤����ABE=��CDF��



 ��ͼ����ABC�У�DE��ֱƽ��BC������ABD���ܳ�Ϊ10��AB=4����AC=6��
��ͼ����ABC�У�DE��ֱƽ��BC������ABD���ܳ�Ϊ10��AB=4����AC=6��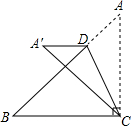 ��ͼ��Rt��ABC�У�BC=AC=2��D��б��AB��һ�����㣬�ѡ�ACD��ֱ��CD�۵�����A����ͬһƽ���ڵ�A�䴦����A��Dƽ����Rt��ABC��ֱ�DZ�ʱ��AD�ij�Ϊ2��2$\sqrt{2}$-2��
��ͼ��Rt��ABC�У�BC=AC=2��D��б��AB��һ�����㣬�ѡ�ACD��ֱ��CD�۵�����A����ͬһƽ���ڵ�A�䴦����A��Dƽ����Rt��ABC��ֱ�DZ�ʱ��AD�ij�Ϊ2��2$\sqrt{2}$-2��