题目内容
15.关于x的方程kx2+(2k+1)x+k-1=0的根都是正整数,则k的值为0,1.分析 分k=0和k≠0两种情况讨论.当k=0时,所给方程为x-1=0,有整数根x=1;当k≠0时,所给方程为二次方程,根据根与系数的关系即可求出k的值,然后用△>0验证k是否符合题意即可.
解答 解:当k=0,方程变为:x-1=0,解得方程有正整数根为x=1;
当k≠0,△=(2k+1)2-4×k×(k-1)=-3k2+6k+1=8k+1,
一元二次方程都是正整数根,则△必须为完全平方数,
当△=9,则k=1;
当△=4,则k=$\frac{3}{8}$,
当△=16时,k=$\frac{15}{8}$;
当△=0,则k=-$\frac{1}{8}$;
而x=$\frac{-(2k+1)±\sqrt{8k+1}}{2k}$,
当k=1,解得x=0或-3;
当k=$\frac{3}{8}$,解得x=-$\frac{1}{7}$或-$\frac{15}{7}$;
当k=$\frac{15}{8}$,解得x=$\frac{1}{5}$或-$\frac{7}{3}$;
当k=-$\frac{1}{8}$,
解得x都不为整数,并且k为其它数△为完全平方数时,解得x都不为整数.
∴当k为0、1关于x的方程kx2+(2k+1)x+k-1=0的根都是正整数.
故答案为:0,1.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了分类讨论思想的运用以及一元二次方程都为整数根的必要条件就是判别式为完全平方数.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
5.下列运算中,正确的是( )
| A. | $\sqrt{9}=±3$ | B. | (a2)3=a6 | C. | 3a•2a=6a | D. | 3-2=-6 |
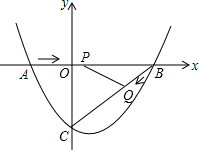 如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.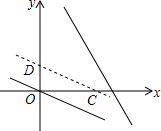 已知:点P是一次函数y=-3x+6图象在y右轴侧部分上的一个动点,将直线y=-$\frac{1}{2}$x沿y轴向上平移,分别交x轴,y轴于C、D两点.
已知:点P是一次函数y=-3x+6图象在y右轴侧部分上的一个动点,将直线y=-$\frac{1}{2}$x沿y轴向上平移,分别交x轴,y轴于C、D两点.