题目内容
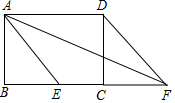
9.已知:正方形ABCD中,点E是BC上一动点(与点B、C不重合),连接AE延长CD到F,使得DF=BE,连接AF,EF,过点A作AP⊥EF,连接PD.
(1)如图1,若点E运动到边BC的延长线上时,判断△AEF的形状,并说明理由;
(2)如图1,若点E运动到边BC的延长线上,求证:∠PDF=45°;
(3)如图2,若点E运动到边BC之间使得∠AEB=60°,求∠APD的度数.
分析 (1)结论:△AEF是等腰直角三角形.只要证明△ABE≌△ADF,推出∠BAE=∠DAF,AE=AF,推出∠EAF=∠BAD=90°,即可证明.
(2)只要证明△AOD∽△FOP,得$\frac{OA}{OF}$=$\frac{OD}{OP}$,即$\frac{OA}{OD}$=$\frac{OF}{OP}$由∠AOF=∠POD,推出△AOF∽△DOP,推出∠PDO=∠FAO=45°,即可解决问题.
(3)首先证明△ABE≌△ADF,推出∠DAF=∠BAE=30°,由△AOF∽△POD,推出∠DPO=∠FAO=30°,即可解决问题.
解答 解:(1)结论:△AEF是等腰直角三角形.
理由:如图1中,
∵四边形ABCD是正方形,
∴AD=AB,∠ABE=∠BAD=∠ADF=90°,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,AE=AF,
∴∠EAF=∠BAD=90°,
∴△AEF是等腰直角三角形.
(2)如图1中,
∵△AEF是等腰三角形,AP⊥EF,
∴PF=PE,
∴PF=PE=AP,
∴∠FAO=45°,
∵∠ADO=∠OPF,∠AOD=∠FOP,
∴△AOD∽△FOP,
∴$\frac{OA}{OF}$=$\frac{OD}{OP}$,
∴$\frac{OA}{OD}$=$\frac{OF}{OP}$,∵∠AOF=∠POD,
∴△AOF∽△DOP,
∴∠PDO=∠FAO=45°,
∴∠PDF=45°
(3)如图2中,
∵四边形ABCD是正方形,
∴AD=AB,∠ABE=∠BAD=∠ADF=90°,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,AE=AF,
∴∠EAF=∠BAD=90°,
∴△AEF是等腰直角三角形,
∵∠AEB=60°∴∠BAE=∠DAF=30°,
∵AP⊥EF,
∠APO=∠ODF=90°,∠AOP=∠FOD,
∴△AOD∽△FOP,
∴$\frac{OA}{OF}$=$\frac{OP}{OD}$,
∴$\frac{OA}{OP}$=$\frac{OF}{OD}$,∵∠AOF=∠POD,
∴△AOF∽△POD,
∴∠DPO=∠FAO=30°,
∴∠APD=∠APF+∠FPD=90°+30°=120°
点评 本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用相似三角形证明角相等,属于中考压轴题.

| A. | y=(x+3)2+3 | B. | y=(x+3)2-1 | C. | y=(x-3)2+3 | D. | y=(x-3)2-1 |
 如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | 5 | D. | $2\sqrt{5}$ |
| A. | 2016年杨家坪房价一定下降 | |
| B. | 两个负数相乘,结果是正数 | |
| C. | 九龙坡区明天一定会下雪 | |
| D. | 小明努力学习,这次数学考试一定得满分 |
| A. | (0,0) | B. | (0,6) | C. | (0,0)和(0,6) | D. | (0,0)和(6,0) |
 如图,∠AOC=30°35′15″,∠BOC=80°15′28″,OC平分∠AOD,那么∠BOD等于49°40′13″.
如图,∠AOC=30°35′15″,∠BOC=80°15′28″,OC平分∠AOD,那么∠BOD等于49°40′13″.