Question

17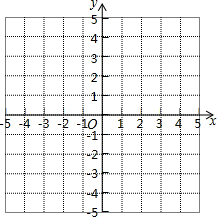．一次函数y₁=x-2与二次函数y₂=ax²+bx+c的图象交于A（2，m）、B（n，3）两点，且抛物线的对称轴为直线x=3．
（1）求二次函数的解析式；
（2）在同一直角坐标系中画出两个函数的图象；
（3）从图象上观察，x取何值时，y₁和y₂都随x的增大而增大；
（4）从图象上观察，x取何值时，y₁＞y₂．

Answer 1

分析 （1）把A（2，m）、B（n，3）分别代入y₁=x-2中解得m=0，n=5，所以求得A（2，0）、B（5，3），将A、B的坐标代入y₂=ax²+bx+c，由抛物线的对称轴为直线x=3得出-$\frac{b}{2a}$=3，列出关于a、b、c的三元一次方程组，进而求出二次函数解析式；
（2）利于描点的方法和函数图象的对称性作图即可；
（3）根据根据一次函数与二次函数的性质，可得当x≥3时，y₁和y₂都随x的增大而增大；
（4）观察图象，可知当2＜x＜5时，一次函数的图象在二次函数图象的上方，即y₁＞y₂．

解答 解：（1）∵一次函数y₁=x-2与二次函数y₂=ax²+bx+c的图象交于A（2，m）、B（n，3）两点，
∴把A、B的坐标代入y₁=x-2得：m=2-2=0，3=n-2，
解得：m=0，n=5，
∴A（2，0）、B（5，3），
∵抛物线的对称轴为直线x=3，
代入二次函数的解析式得：
$\left\{\begin{array}{l}{4a+2b+c=0}\\{25a+5b+c=3}\\{-\frac{b}{2a}=3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=-6}\\{c=8}\end{array}\right.$．
∴二次函数的解析式为y₂=x²-6x+8；

（2）两个函数的图象如图所示：


（3）从图象上观察：当x≥3时，y₁和y₂都随x的增大而增大；

（4）当2＜x＜5时，y₁＞y₂．

点评 本题主要考查了待定系数法求二次函数的解析式，一次函数与二次函数图象的性质及其作图．要注意：当a＞0时，图象开口向上，在对称轴的右侧y随x的增大而增大，在对称轴的左侧y随x的增大而减小．