题目内容
6．已知关于x的方程x2+mx+12=0的两个根是x1、x2，方程x2-mx+n=0的两实数根是x1+7，x2+7，求m，n的值．分析 由关于x的方程x2+mx+12=0的两个根是x1、x2，得出x1+x2=-m，x1•x2=12；同理方程x2-mx+n=0的两实数根是x1+7，x2+7，得出出x1+x2=m-14，（7+x1）（7+x2）=n；进一步整理得出答案即可．
解答 解：∵关于x的方程x2+mx+12=0的两个根是x1、x2，方程x2-mx+n=0的两实数根是x1+7，x2+7，
∴x1+x2=-m，x1•x2=12；x1+x2=m-14，（7+x1）（7+x2）=49+7（x1+x2）+x1•x2=n；
∴-m=m-14，m=7，n=49+7×（-7）+12=12．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
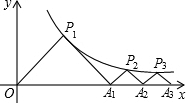如图，点P1（x1，y1），点P2（x2，y2），P3（x3，y3）都在函数y=$\frac{k}{x}$（x＞0）的图象上，△P1OA1，△P2A1A2，△P3A2A3，都是等腰直角三角形，斜边OA3，A1A2，A2A3都在x轴上，已知点P1的坐标为（1，1），则点P3的坐标为（$\sqrt{3}$+$\sqrt{2}$，$\sqrt{3}$-$\sqrt{2}$）．
3．
一项工程，甲、乙两人合作5h后，甲被调走，剩余的部分由乙继续完成，设这项工程的全部工作量为1，工作量与工作时间之间的函数关系式如图所示，那么甲的工作效率是（ ）
一项工程，甲、乙两人合作5h后，甲被调走，剩余的部分由乙继续完成，设这项工程的全部工作量为1，工作量与工作时间之间的函数关系式如图所示，那么甲的工作效率是（ ）| A． | $\frac{1}{10}$ | B． | $\frac{1}{15}$ | C． | $\frac{1}{20}$ | D． | $\frac{1}{30}$ |
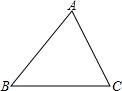如图，在△ABC中，画出它们的三条中线AD、BE、CF，三条中线交于一点G，AG与GD的长度有什么关系？用刻度尺验证你的结论，换一个三角形试试看，上述结论是否还成立？
如图，P是△ABC内一点，试说明2（PA+PB+PC）＞（AB+BC+AC）