题目内容
1．解方程：$\frac{3}{（x-1）（x+2）}+1=\frac{x}{x-1}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：方程两边同乘（x-1）（x+2），得3+（x-1）（x+2）=x（x+2），
解得：x=1，
检验：当x=1时，（x-1）（x+2）=0，故x=1不是原分式方程的解，
则原分式方程无解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
口算题天天练系列答案
相关题目
11．
右边几何体的俯视图是（ ）
右边几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
16．下列计算正确的是（ ）
| A． | x6÷x2=x3 | B． | $3{m^{-2}}=\frac{1}{{3{m^2}}}$ | C． | （a3b）2=a6b2 | D． | （a2）4=a6 |
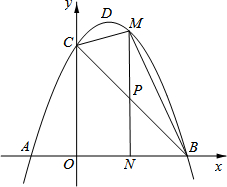如图，抛物线y=-x2+bx+c的顶点为D，与x轴交于A（-1，0）、B（3，0），与y轴交于点C．
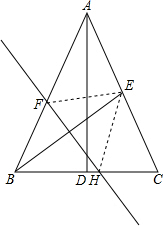如图，在△ABC中，AB=AC，底边BC上的高AD=12，tan C=2，如果将△ABC沿直线l翻折后，点B刚好落在AC边的中点E处，直线l与边AB交于点F，与边BC交于点H，求BH的长．
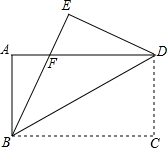如图，沿矩形ABCD的对角线BD折叠，点C落在点E的位置，已知BC=8cm，AB=6cm，那么折叠后的重合部分的面积是多少？