题目内容
17. 已知,∠AOB=30°,点M1,M2,M3…在射线OB上,点N1,N2,N3…在射线0A上,△M1N1M2,△M2N2M3,△M3N3M4…均为等边三角形.若OM1=1,则△MnNnMn+1的边长为( )
已知,∠AOB=30°,点M1,M2,M3…在射线OB上,点N1,N2,N3…在射线0A上,△M1N1M2,△M2N2M3,△M3N3M4…均为等边三角形.若OM1=1,则△MnNnMn+1的边长为( )| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 2n |
分析 根据等腰三角形的性质求出△M1N1M2的边长,根据直角三角形的性质求出△M2N2M3的边长,总结规律得到答案.
解答 解:∵,△M1N1M2是等边三角形,∴∠N1M1M2=60°,
∴∠ON1M1=30°,
∴N1M1=OM1=1=20,
∵∠ON1M1=30°,M1N1M2=60°,
∴∠M2N1N2=90°,∠N1N2M2=30°,
∴N2M2=2N1M2=2=21,
同理M3N3=2N2M3=4=22,
以此类推,△MnNnMn+1的边长为:2n-1,
故选:C.
点评 本题考查的是等边三角形的性质和直角三角形的性质,掌握在直角三角形中,30°的直角边是斜边的一半是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
7.下列调査中,适合采用全面调査(普査)方式的是( )
| A. | 调査某池塘中现有鱼的数量 | |
| B. | 对端午节期间市场上粽子质量情况的调査 | |
| C. | 企业招聘,对应聘人员进行面试 | |
| D. | 对某类烟花爆竹燃放安全情况的调査 |
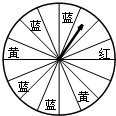 如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.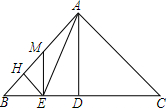 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,EH⊥AB,垂足是H.在AB上取一点M,使BM=2DE,连接ME.求证:ME⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,EH⊥AB,垂足是H.在AB上取一点M,使BM=2DE,连接ME.求证:ME⊥BC.