��Ŀ����
9�� ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\sqrt{3}$x+3$\sqrt{3}$��x���ڵ�A����y���ڵ�B���ҡ�ABO=30�㣬����P��A�㿪ʼ��AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ1��$\sqrt{3}$��2�����ȵ�λ/�룩��ֱ��l����x���غϵ�λ�ÿ�ʼ��$\frac{\sqrt{3}}{3}$�����ȵ�λ/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F���㣬�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P��AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\sqrt{3}$x+3$\sqrt{3}$��x���ڵ�A����y���ڵ�B���ҡ�ABO=30�㣬����P��A�㿪ʼ��AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ1��$\sqrt{3}$��2�����ȵ�λ/�룩��ֱ��l����x���غϵ�λ�ÿ�ʼ��$\frac{\sqrt{3}}{3}$�����ȵ�λ/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F���㣬�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P��AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶��������������⣺
��1����գ�
�ٵ�A�����꣨3��0������B�����꣨0��3$\sqrt{3}$����
�ڵ�t=4ʱ����P������Ϊ��0��$\sqrt{3}$����
��2����tΪ��ֵʱ����P���E�غϣ�
��3����tΪ��ֵʱ����PEF����EFΪ�ױߵĵ��������Σ�
���� ��1�������������ϵ���ص���⼴�ɣ�
�����жϳ�t=4ʱ����P��λ�ã�����Ҫ���յ�P���˶�·�ߣ�Ҫ���յ�P�ڲ�ͬ�ε��˶��ٶȣ�������ã�
��2�����жϳ���P�͵�E�غ�ʱ����P�߹���·�������E�߹���·�����OA=3���ٽ���������⼴�ɣ�
��3������������������ۼ��㣬��ƽ������ϵ�������ľ��빫ʽ��PE=PF����������⼴�ɣ�
��� �⣺��1���١�ֱ��y=-$\sqrt{3}$x+3$\sqrt{3}$��x���ڵ�A����y���ڵ�B��
����x=0����y=3$\sqrt{3}$��
��y=0����x=3��
��A��3��0����B��0��3$\sqrt{3}$����
�ʴ�Ϊ��3��0������0��3$\sqrt{3}$����
�ڡߵ�A�������ǣ�3��0����
��OA=3��
�֡ߵ�P��AO��OB��BA���˶����ٶȷֱ�Ϊ1��$\sqrt{3}$��
�൱t=4ʱ����P���߶�OB�ϣ���OP=��4-3��1����$\sqrt{3}$=$\sqrt{3}$��
���P�������ǣ�0��$\sqrt{3}$����
�ʴ�Ϊ��0��$\sqrt{3}$��
��2������P���E�غ�ʱ��$\frac{OE}{\frac{\sqrt{3}}{3}}=\frac{OE}{\sqrt{3}}+\frac{OA}{1}=\frac{OE}{\sqrt{3}}+3$��
��OE=$\frac{3\sqrt{3}}{2}$��
��t=$\frac{\frac{3\sqrt{3}}{2}}{\frac{\sqrt{3}}{3}}$=$\frac{9}{2}$��
��3����A��3��0����B��0��3$\sqrt{3}$����
��OA=3��OB=3$\sqrt{3}$��
���ݹ��ɶ����ã�AB=6��
ֱ��l��x���˶�������Bʱ����ʱ��Ϊ3$\sqrt{3}$��$\frac{\sqrt{3}}{3}$=9s
�ߵ�P��AO��OB��BA���˶����ٶȷֱ�Ϊ1��$\sqrt{3}$��2��
���P�˶�һ������ʱ��Ϊ3��1+3$\sqrt{3}$��$\sqrt{3}$+6��2=9s��
���P��ֱ��lͬʱ�˶�ͬʱֹͣ��
�ߡ�PEF����EFΪ�ױߵĵ��������Σ�
��PE=PF��
�ٵ���P���߶�OA��ʱ����0��t��3��
��P��3-t��0������E��0��$\frac{\sqrt{3}}{3}$t����
��ֱ��y=-$\sqrt{3}$x+3$\sqrt{3}$��x���ڵ�A����y���ڵ�B��
����y=$\frac{\sqrt{3}}{3}$t��
��x=3-$\frac{1}{3}$t��
��F��3-$\frac{1}{3}$t��$\frac{\sqrt{3}}{3}$t����
��PE=PF��
��PE2=PF2��
�ࣨ3-t��2+��$\frac{\sqrt{3}}{3}$t��2=[3-$\frac{1}{3}$t-��3-t��]2+��$\frac{\sqrt{3}}{3}$t��2��
��t=9���ᣩ��t=$\frac{9}{5}$��
�ڵ���P���߶�OB��ʱ����3��t��6ʱ��
�ߡ�OEF=90�㣬
���ʱ�����ܹ�����EFΪ�ĵ��������Σ�
�۵���P���߶�AB��ʱ������6��t��9��
���P����a�뵽���A�����P�˶���9-a=t����0��a��3��
��ֱ��l�˶���9-a�룬BP=6-2a
��E��0��$\frac{\sqrt{3}}{3}$��9-a������
��ֱ��AB����ʽΪy=-$\sqrt{3}$x+3$\sqrt{3}$����EF��x�ᣬ
��F��$\frac{1}{3}$a��$\frac{\sqrt{3}}{3}$��9-a����
���˶��У�BP=6-2a
��PG=3-a��BG=$\sqrt{3}$��3-a����
��P��3-a��$\sqrt{3}$��3-a������
��PE=PF��
��PE2=PF2��
�ࣨ3-a��2+[$\sqrt{3}$��3-a��-$\frac{\sqrt{3}}{3}$��9-a��]2=��3-a-$\frac{1}{3}$a��2+[$\sqrt{3}$��3-a��-$\frac{\sqrt{3}}{3}$��9-a��]2��
��a=0���ᣩ��a=$\frac{18}{7}$��
��t=9-a=9-$\frac{18}{7}$=$\frac{45}{7}$��
����t=$\frac{9}{5}$��t=$\frac{45}{7}$��ʱ����PEF����EFΪ�ױߵĵ��������Σ�
���� ������һ�κ����ۺ��⣬��Ҫ�������������ϵ���ص㣬����˼���������ǽⱾ��Ĺؼ�Ҳ���ѵ㣮

| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
| ���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
| �����仯 ���ˣ� | +31 | +178 | -58 | -8 | -1 | -16 | -115 |
��2��������ο�����������10��2�գ��ﵽ1209�ˣ��ο��������ٵ���10��7�գ��ﵽ1011�ˣ�
��3�������齭Դͷ�羰�����������һ���Ӵ��˶����οͣ�
| A�� | ֵ����ʦ�������ij�ȱ��ѧ����� | |
| B�� | ����ij�ּҾߵĹ˿�������� | |
| C�� | ����ij�ֱָʵ�ʹ����� | |
| D�� | �˽��ļ������г��ϱ���ܵ�������� |
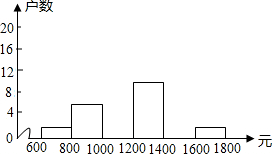 �����������40�������ͥ�������������ȡ��������λ��Ԫ��������������ͼ��Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�����������40�������ͥ�������������ȡ��������λ��Ԫ��������������ͼ��Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�� | ���� | Ƶ�� | �ٷֱ� |
| 600��x��800 | 2 | 5% |
| 800��x��1000 | 6 | 15% |
| 1000��x��1200 | 45% | |
| 9 | 22.5% | |
| 1600��x��1800 | 2 | |
| �ϼ� | 40 | 100% |
��1����ȫƵ���ֲ�����
��2����ȫƵ��ֱ��ͼ��
��3�����Ƹþ���С����ͥ�����е����루���ڵ���1000����1600Ԫ���Ĵ�Լ�ж��ٻ���
 ��֪����ͼ����ADE=46�㣬DFƽ�֡�ADE����1=23�㣬��֤��DF��BE��
��֪����ͼ����ADE=46�㣬DFƽ�֡�ADE����1=23�㣬��֤��DF��BE��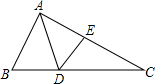 ��ͼ���ڡ�ABC�У���֪AD�ǡ�BAC�Ľ�ƽ���ߣ���B=65�㣬��C=54��
��ͼ���ڡ�ABC�У���֪AD�ǡ�BAC�Ľ�ƽ���ߣ���B=65�㣬��C=54��