题目内容
1. 如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值;
(3)若ED=4,EA=2求直径AB的长.
分析 (1)首选连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线;
(2)由△COD≌△COB可得CD=CB,即可得DE=2CD,易证得△EDA∽△ECO,然后由相似三角形的对应边成比例,求得AD:OC的值;
(3)根据切割线定理得出EB,即可求得AB的长.
解答 (1)证明:连结DO.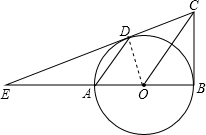
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中,
$\left\{\begin{array}{l}{CO=CO}\\{∠COD=∠COB}\\{OD=OB}\end{array}\right.$,
∴△COD≌△COB(SAS)
∴∠CDO=∠CBO=90°.
又∵点D在⊙O上,
∴CD是⊙O的切线.
(2)解:∵△COD≌△COB.
∴CD=CB.
∵DE=2BC,
∴ED=2CD.
∵AD∥OC,
∴△EDA∽△ECO.
∴$\frac{AD}{OC}$=$\frac{2}{3}$.
(3)∵CD是⊙O的切线,
∴ED2=EA•EB,
∵ED=4,EA=2,
∴42=2EB,
∴EB=8,
∴AB=EB-EA=8-2=6.
点评 此题考查了切线的判定、全等三角形的判定与性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
12.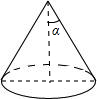 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
 B.
B. 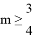 C.
C. 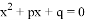 的两根分别为
的两根分别为 ,
,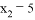 ,那么这个一元二次方程是______.
,那么这个一元二次方程是______.