题目内容
10．
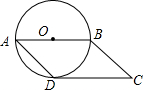如图，若以平行四边形一边AB为直径的圆恰好与边CD相切于点D，则∠C的度数是（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 60° |
分析 连接OD，如图，先利用切线的性质得OD⊥CD，再根据平行四边形的性质∠A=∠C，AB∥CD，则OD⊥AB，利用圆周角定理得到∠A=$\frac{1}{2}$∠BOD=45°，从而得到∠C的度数．
解答 解：连接OD，如图，
∵CD为切线，
∴OD⊥CD，
∵四边形ABCD为平行四边形，
∴∠A=∠C，AB∥CD，
∴OD⊥AB，
∴∠BOD=90°，
∴∠A=$\frac{1}{2}$∠BOD=45°，
∴∠C=45°．
故选B．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了平行四边形的性质．
练习册系列答案
相关题目
10．正方形具有而菱形不一定具有的性质是（ ）
| A． | 对角线平分一组对角 | B． | 对角线互相垂直平分 | ||
| C． | 对角线相等 | D． | 四条边相等 |
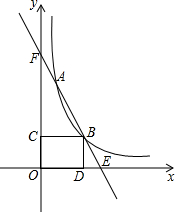如图，直线y=-2x+b（b＞0）交两坐标轴于点E、F，交反比例函数y=$\frac{k}{x}$（x＞0，k＞0）的图象于点A，B，BC⊥y轴于点C，BD⊥x轴于点D，若2BC-BD=2，则AB的长为$\sqrt{5}$．
5．下列各式计算正确的是（ ）
| A． | a2×a3=a6 | B． | $\sqrt{\frac{3}{2}}÷\sqrt{2}=\frac{{\sqrt{3}}}{2}$ | C． | $\frac{x-1}{{1-{x^2}}}=\frac{1}{x+1}$ | D． | （x+y）2=x2+y2 |
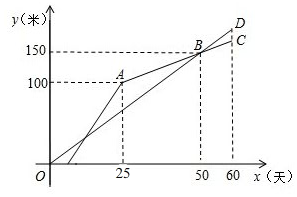甲、乙两个工程队共同修建一条乡镇公路，甲队按一定的工作效率先施工，一段时间后，乙队从另一端按一定的工作效率加入施工，中途乙队遇到山坡路段，工作效率降低，当乙队完成山坡路段时恰好公路修建完成，此时甲队工作了60天，设甲、乙两队各自修建的公路的长度为y（米），甲队工作时间为x（天），y与x之间的函数图象如图所示．