题目内容
4.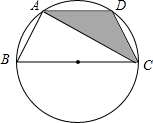 如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.
如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.
分析 连接OA、OD,则阴影部分的面积等于梯形的面积减去三角形的面积.根据题目中的条件不难发现等边三角形AOD、AOB、COD,从而求解.
解答  解:设圆心为O,连接OA、OD.
解:设圆心为O,连接OA、OD.
∵AD∥BC,AC平分∠BCD,∠ADC=120°,
∴∠BCD=60°,
∵AC平分∠BCD,
∴∠ACD=30°,
∴∠AOD=2∠ACD=60°,∠OAC=∠ACO=30°.
∴∠BAC=90°,
∴BC是直径,
又∵OA=OD=OB=OC,
则△AOD、△AOB、△COD都是等边三角形.
∴AB=AD=CD.
又∵四边形ABCD的周长为10cm,
∴OB=OC=AB=AD=DC=2(cm).
∴阴影部分的面积=S梯形-S△ABC=$\frac{1}{2}$(2+4)×$\sqrt{3}$-$\frac{1}{2}$×4×$\sqrt{3}$=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 此题综合考查了梯形的面积,三角形的面积以及等边三角形的判定和性质.作出辅助线构建等边三角形是解题的关键.

练习册系列答案
相关题目
14.下列命题中假命题是( )
| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
15.某工地因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
19.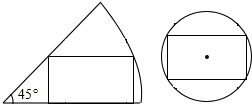 一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
 一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )| A. | 2$\sqrt{2}$:1 | B. | $\sqrt{5}$:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
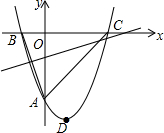 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点