题目内容
已知一元二次方程的两个根是x1，x2，且x1=2x2，那么这个方程可以是 （填上你认为正确的一个方程即可）
考点：根与系数的关系
专题：开放型
分析：由于关于x的一元二次方程的两个根分别为x1，x2，且x1=2x2，则x1+x2=3x1，x1x2=2x12，根据此条件即可求出方程．
解答：解：设一元二次方程有一个根是x1=1，
∴x1+x2=3x1=3，x1x2=2x12=2
∴方程可以为x2-3x+2=0，
故答案为：x2-3x+2=0．
∴x1+x2=3x1=3，x1x2=2x12=2
∴方程可以为x2-3x+2=0，
故答案为：x2-3x+2=0．
点评：此题考查了一元二次方程根与系数的关系，一元二次方程有解时，设为x1，x2，方程可为x2-（x1+x2）x+x1x2=0．
练习册系列答案
相关题目
若多项式-4x3-2mx2+6x2-6合并同类项后的是一个三次二项式，则m满足的条件（ ）
| A、m=3 | B、m=-3 |
| C、m≠3 | D、m≠-3 |
一块面积是600m2的长方形土地，它的长比宽多10m，设宽为x，则可列方程为（ ）
| A、x2-10x+600=0 |
| B、x2+10x-600=0 |
| C、x（x-10）=600 |
| D、x（x+10）+600=0 |
如图，△ABC≌△ADE，AB和AD，AC和AE是对应边，那么∠DAC等于（ ）| A、∠ACB | B、∠CAE |
| C、∠BAE | D、∠BAC |
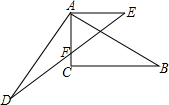已知如图，AC=AE，AD=AB，∠ACB=∠DAB=90°，AE∥CB，AC、DE交于点F．