题目内容
两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则较大的五边形面积是 cm2.
考点:相似多边形的性质
专题:
分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.
解答:解:设较大五边形与较小五边形的面积分别是m,n.则
=(
)2=
.
因而n=
m.
根据面积之和是78cm2.得到m+
m=78.
解得:m=54cm2.
故答案为:54.
| m |
| n |
| 3 |
| 4.5 |
| 4 |
| 9 |
因而n=
| 4 |
| 9 |
根据面积之和是78cm2.得到m+
| 4 |
| 9 |
解得:m=54cm2.
故答案为:54.
点评:本题考查相似多边形的性质.面积之比等于相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC≌△ADE,AB和AD,AC和AE是对应边,那么∠DAC等于( )
如图,△ABC≌△ADE,AB和AD,AC和AE是对应边,那么∠DAC等于( )| A、∠ACB | B、∠CAE |
| C、∠BAE | D、∠BAC |
下列调查中,样本最具有代表性的是( )
| A、在重点中学调查全市七年级学生的数学水平 |
| B、在篮球场上调查青少年对我国篮球事业的关注度 |
| C、了解班上学生的睡眠时间时,调查班上学好为双的学生的睡眠时间 |
| D、了解某人心地是否善良,调查他对子女的态度 |
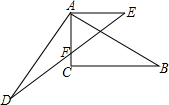 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
 如图,把边长为3cm的等边三角绕其中心沿逆时针方向旋转180°后,旋转前后两三角形重叠部分的面积为
如图,把边长为3cm的等边三角绕其中心沿逆时针方向旋转180°后,旋转前后两三角形重叠部分的面积为