题目内容
19. 如图,四边形ABCD是菱形,过点A、C作对角线AC的垂线,分别交CD和AB的延长线于点E、F.已知AE=2,四边形AECF的周长为12,则菱形的边长为( )
如图,四边形ABCD是菱形,过点A、C作对角线AC的垂线,分别交CD和AB的延长线于点E、F.已知AE=2,四边形AECF的周长为12,则菱形的边长为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 由EA⊥AC,FC⊥AC,可得AE∥CF,又由四边形ABCD是菱形,可得AF∥CE,即可证得四边形AECF是平行四边形,又由AE=2,四边形AECF的周长为12,即可求得CE的长,易得∠EAD=∠AEC,即可证得AD=DF=DC,继而求得答案.
解答 解:∵EA⊥AC,FC⊥AC,
∴AE∥CF,
∵四边形ABCD是菱形,
∴AF∥CE,
∴四边形AECF是平行四边形,
∴四边形AECF的周长为12,AE=2,
∴CE=4,
∵∠DAC=∠DCA,∠EAD+∠DAC=90°,∠AEC+∠DCA=90°,
∴∠EAD=∠AEC,
∴AD=DF=DC,
∴DC=$\frac{1}{2}$CE=2.
故选A.
点评 此题考查了菱形的性质以及平行四边形的判定与性质.注意证得四边形AECF是平行四边形以及AD=DE=DC是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列直线表示的不是y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
14.A、B、C、D、E五名同学在一次数学测验中的平均成绩是80分,而A、B、C三人的平均成绩是78分,下列说法一定正确的是( )
| A. | D、E的成绩比其他三人都好 | |
| B. | D、E两人的平均成绩是83分 | |
| C. | 五人成绩的中位数一定是其中一人的成绩 | |
| D. | 五人的成绩的众数一定是80分 |
 如图,AB∥CD,∠A=32°,∠C=70°,则∠F=38°.
如图,AB∥CD,∠A=32°,∠C=70°,则∠F=38°.
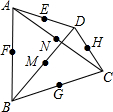 如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形,最多可以有几个平行四边形?证明你的结论.
如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形,最多可以有几个平行四边形?证明你的结论.