题目内容
12.若圆O的半径是5,圆心的坐标是(0,0),点P的坐标是(-4,3),则点P与⊙O的位置关系是点P在圆O上.分析 先利用两点间的距离公式计算出OP的长,然后根据点与圆的位置关系判断点P与⊙O的位置关系.
解答 解:∵点P的坐标是(-4,3),
∴OP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵OP等于圆O的半径,
∴点P在圆O上.
故答案为点P在圆O上.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.△ABC是不规则三角形,若线段AD把△ABC分为面积相等的两部分,则线段AD应该是( )
| A. | 三角形的角平分线 | B. | 三角形的中线 | ||
| C. | 三角形的高 | D. | 以上都不对 |
4.下列各组是同类项的是( )
| A. | 5xy与2x | B. | 0与-7 | C. | -2x2y与5y2z | D. | 3ac与7bc |
 如图所示的立方体的六个面分别标着连续的整数,则这六个数的和为27或33或39.
如图所示的立方体的六个面分别标着连续的整数,则这六个数的和为27或33或39. 如图,△ABC内接于⊙O,⊙O的半径为6,连接OB、OC.若∠BAC与∠BOC互补,求弦BC的长.
如图,△ABC内接于⊙O,⊙O的半径为6,连接OB、OC.若∠BAC与∠BOC互补,求弦BC的长.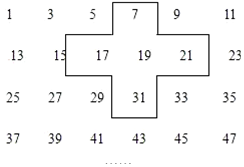 实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)
实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)