题目内容
如图,△ABC中,AB=AC,∠BAC=90°,点D在CB上,连接AD,EA⊥AD,∠ACE=∠ABD.
(1)求证:AD=AE;
(2)若点F为CD中点,AF交BE于点G,求∠AGE的度数.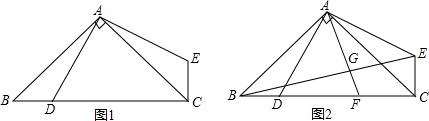
(1)求证:AD=AE;
(2)若点F为CD中点,AF交BE于点G,求∠AGE的度数.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据∠BAC=90°,EA⊥AD,可得∠BAD=∠CAE,然后根据AB=AC,∠ACE=∠ABD,可证明△ABD≌△ACE,继而可得出AD=AE;
(2)延长AF至M,使FM=AF,连接MC,易证△ADF≌△MCF,可得出AD=AE=CM,易证∠BAE=∠ACM,从而证得△ABE≌△CAM,通过∠ABG=∠CAF,得到∠AGE=90°.
(2)延长AF至M,使FM=AF,连接MC,易证△ADF≌△MCF,可得出AD=AE=CM,易证∠BAE=∠ACM,从而证得△ABE≌△CAM,通过∠ABG=∠CAF,得到∠AGE=90°.
解答:解:(1)∵∠BAC=90°,EA⊥AD,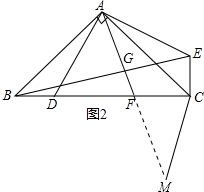
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(ASA),
∴AD=AE;
(2)延长AF至M,使FM=AF,连接MC,
在△ADF与△MCF中,
,
∴△ADF≌△MCF(SAS),
∴AD=CM,
∵△ABD≌△ACE,
∴AD=AE,
∴AD=AE=CM,
∴∠BAM=∠CAM,
在△ABE和△CAM中,
,
∴△ABE≌△CAM(ASA),
∴∠ABG=∠CAF,
∵∠CAF+∠BAG=90°,
∴∠ABG+∠BAG=90°,
∴∠AGB=∠AGE=90°.

∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(ASA),
∴AD=AE;
(2)延长AF至M,使FM=AF,连接MC,
在△ADF与△MCF中,
|
∴△ADF≌△MCF(SAS),
∴AD=CM,
∵△ABD≌△ACE,
∴AD=AE,
∴AD=AE=CM,
∴∠BAM=∠CAM,
在△ABE和△CAM中,
|
∴△ABE≌△CAM(ASA),
∴∠ABG=∠CAF,
∵∠CAF+∠BAG=90°,
∴∠ABG+∠BAG=90°,
∴∠AGB=∠AGE=90°.
点评:本题考查了全等三角形的判定和性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
下列各近似数中,精确度一样的是( )
| A、0.28与0.280 |
| B、0.70与0.07 |
| C、5百万与500万 |
| D、1.1×103与1100 |
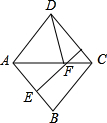 如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )| A、100° | B、104° |
| C、105° | D、110° |
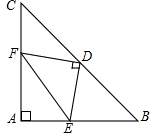 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
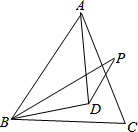 如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.求证:∠BPD=30°.
如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.求证:∠BPD=30°. 如图所示,D是AB的中点,E是BC的中点,BE=
如图所示,D是AB的中点,E是BC的中点,BE=