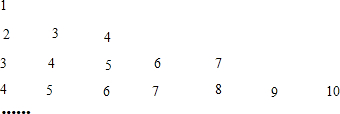题目内容
9.先化简,再求值:$\frac{1}{2}$x-2(x-$\frac{1}{3}$y4)+(-$\frac{3}{2}$x+$\frac{1}{3}$y4),其中x,y满足(x-2)2+|y+1|=0.分析 首先去括号进而合并同类项,再利用绝对值和偶次方的性质得出x,y的值,进而得出答案.
解答 解:$\frac{1}{2}$x-2(x-$\frac{1}{3}$y4)+(-$\frac{3}{2}$x+$\frac{1}{3}$y4)
=$\frac{1}{2}$x-2x+$\frac{2}{3}$y4-$\frac{3}{2}$x+$\frac{1}{3}$y4,
=-3x+y4,
∵(x-2)2+|y+1|=0,
∴x-2=0,y+1=0,
解得:x=2,y=-1,
∴原式=-3×2+(-1)4=-5.
点评 此题主要考查了整式的加减运算,正确合并同类项是解题关键.

练习册系列答案
相关题目
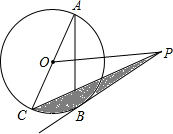 已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.
已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.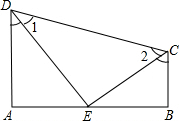 如图:已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°
如图:已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90° 如图所示是用棋子摆成的“小雨伞”:摆第一个“小雨伞”用了9个棋子,摆第二个“小雨伞”用了12个棋子,摆第三个“小雨伞”用了15个棋子,…依次规律,用75个棋子摆成的“小雨伞”是第几个图形( )
如图所示是用棋子摆成的“小雨伞”:摆第一个“小雨伞”用了9个棋子,摆第二个“小雨伞”用了12个棋子,摆第三个“小雨伞”用了15个棋子,…依次规律,用75个棋子摆成的“小雨伞”是第几个图形( )