题目内容
 如图,A、B是双曲线y=
如图,A、B是双曲线y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F,那么由AD∥BE,AD=2BE,可知B、E分别是AC、DC的中点,易证△ABF≌△CBE,则S△AOC=S梯形AOEF=3,根据梯形的面积公式即可求出k的值.
解答:解:如图,

分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F.
∴四边形ADEF是矩形,
∵A、B两点的横坐标分别是a、2a,
∴AD∥BE,AD=2BE=
,
∴B、E分别是AC、DC的中点.
在△ABF与△CBE中,∠ABF=∠CBE,∠F=∠BEC=90°,AB=CB,
∴△ABF≌△CBE.
∴S△AOC=S梯形AOEF=3.
又∵A(a,
),B(2a,
),
∴S梯形AOEF=
(AF+OE)×EF=
(a+2a)×
=
=3,
解得:k=2.

分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F.
∴四边形ADEF是矩形,
∵A、B两点的横坐标分别是a、2a,
∴AD∥BE,AD=2BE=
| k |
| a |
∴B、E分别是AC、DC的中点.
在△ABF与△CBE中,∠ABF=∠CBE,∠F=∠BEC=90°,AB=CB,
∴△ABF≌△CBE.
∴S△AOC=S梯形AOEF=3.
又∵A(a,
| k |
| a |
| k |
| 2a |
∴S梯形AOEF=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
| 3k |
| 2 |
解得:k=2.
点评:本题主要考查了反比例函数的性质、三角形的中位线的判定及梯形的面积公式,体现了数形结合的思想.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知函数y=3x2-6x+k(k为常数)的图象经过点A(0.8,y1),B(1.1,y2),C(
,y3),则有( )
| 2 |
| A、y1<y2<y3 |
| B、y1>y2>y3 |
| C、y3>y1>y2 |
| D、y1>y3>y2 |
在数|-4.5|,-|+2.1|,-(-0.8),+|-0|中,负数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
等腰三角形的一个内角是75°,它的顶角是( )
| A、30° | B、75° |
| C、30°或75° | D、105° |
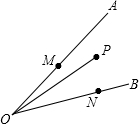 如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是
如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是