Question

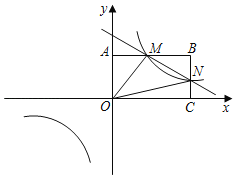
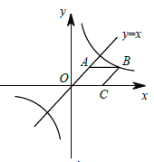
【题目】如图，已知菱形，点在轴上，直线经过点，菱形的面积是. 若反比例函数的图象经过点，则此反比例函数表达式中的为_____.

Answer 1

【答案】

【解析】

作AH⊥x轴于H，如图，利用一次函数图象上点的坐标特征，设A（t，t），利用菱形面积公式得到OC=，则可表示出B（t+，t），然后利用反比例函数函数图象上点的坐标特征可计算出k的值．

解：作AH⊥x轴于H，如图，

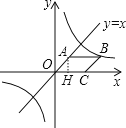
设A（t，t），

由题意，菱形OABC的面积是，

∴tOC=，

∴OC=，

∴菱形OABC中,OA=OC=

∴根据勾股定理: ,解得:

又∵四边形OABC为菱形，

∴AB=，AB∥x轴，

∴B（t+，t），

而B（t+，t）在反比例函数函数的图象上，

∴k=（t+）t=+1．

故答案为：+1．